题目内容
设e1，e2分别为具有公共焦点F1与F2的椭圆和双曲线的离心率，P为两曲线的一个公共点，且满足
•
=0，则
的值为（ ）
| PF1 |
| PF2 |
| e12+e12 |
| (e1e2)2 |
| A、1 | ||
B、
| ||
| C、4 | ||
| D、2 |
考点：双曲线的简单性质,平面向量数量积的运算,椭圆的简单性质
专题：计算题,平面向量及应用,圆锥曲线的定义、性质与方程
分析：设椭圆的长半轴是a1，双曲线的实半轴是a2，它们的半焦距是c，并设PF1=m，PF2=n，m＞n，根据椭圆的和双曲线的定义可得m+n=2a1，m-n=2a2，写出两个曲线的离心率，由向量垂直的条件，运用勾股定理可得等式，代入要求的式子得到结果．
解答：
解：设椭圆的长半轴是a1，双曲线的实半轴是a2，它们的半焦距是c，
并设PF1=m，PF2=n，m＞n，根据椭圆的和双曲线的定义可得
m+n=2a1，m-n=2a2
解得m=a1+a2，n=a1-a2
又PF1⊥PF2，由勾股定理得，
PF12+PF22=F1F22
即（a1+a2）2+（a1-a2）2=（2c）2
化简可得a12+a22=2c2
则
=
+
=
+
=2．
故选D．
并设PF1=m，PF2=n，m＞n，根据椭圆的和双曲线的定义可得
m+n=2a1，m-n=2a2
解得m=a1+a2，n=a1-a2
又PF1⊥PF2，由勾股定理得，
PF12+PF22=F1F22
即（a1+a2）2+（a1-a2）2=（2c）2
化简可得a12+a22=2c2
则
| e12+e12 |
| (e1e2)2 |
| 1 |
| e12 |
| 1 |
| e22 |
| a12 |
| c2 |
| a22 |
| c2 |
故选D．
点评：本题考查圆锥曲线的共同特征，本题解题的关键是得到两个曲线的参数之间的关系，本题是一个基础题．
练习册系列答案
相关题目
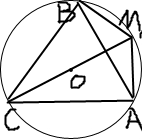如图，在△ABC中，a，b，c分别为∠A，∠B，∠C的对边，a2+b2-c2=ab，CM是△ABC外接圆的直径，BM=11，AM=2，求CM的长．