题目内容
已知函数f(x)=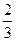 x3-2ax2+3x(x∈R).
x3-2ax2+3x(x∈R).
(1)若a=1,点P为曲线y=f(x)上的一个动点,求以点P为切点的切线斜率取最小值时的切线方程
(2)若函数y=f(x)在(0,+∞)上为单调增函数,试求满足条件的最大整数a.
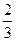 x3-2ax2+3x(x∈R).
x3-2ax2+3x(x∈R). (1)若a=1,点P为曲线y=f(x)上的一个动点,求以点P为切点的切线斜率取最小值时的切线方程
(2)若函数y=f(x)在(0,+∞)上为单调增函数,试求满足条件的最大整数a.
⑴3x-3y+2=0,⑵1
(1)设切线的斜率为k,则k= =2x2-4x+3=2(x-1)2+1, …………2分
=2x2-4x+3=2(x-1)2+1, …………2分
当x=1时,kmin=1.又f(1)= ,所以所求切线的方程为y-
,所以所求切线的方程为y- =x-1,
=x-1,
即3x-3y+2=0. ……………………6分
(2) =2x2-4ax+3,要使y=f(x)为单调递增函数,必须满足
=2x2-4ax+3,要使y=f(x)为单调递增函数,必须满足 >0,即对任意的x∈(0,+∞),恒有
>0,即对任意的x∈(0,+∞),恒有 >0,
>0, =2x2-4ax+3>0, ……………………8分
=2x2-4ax+3>0, ……………………8分
∴a< =
= +
+ ,而
,而 +
+ ≥
≥ ,当且仅当x=
,当且仅当x= 时,等号成立.
时,等号成立.
所以a< ,……………11分
,……………11分
所求满足条件的a值为1 ……………12分
 =2x2-4x+3=2(x-1)2+1, …………2分
=2x2-4x+3=2(x-1)2+1, …………2分当x=1时,kmin=1.又f(1)=
 ,所以所求切线的方程为y-
,所以所求切线的方程为y- =x-1,
=x-1,即3x-3y+2=0. ……………………6分
(2)
 =2x2-4ax+3,要使y=f(x)为单调递增函数,必须满足
=2x2-4ax+3,要使y=f(x)为单调递增函数,必须满足 >0,即对任意的x∈(0,+∞),恒有
>0,即对任意的x∈(0,+∞),恒有 >0,
>0, =2x2-4ax+3>0, ……………………8分
=2x2-4ax+3>0, ……………………8分∴a<
 =
= +
+ ,而
,而 +
+ ≥
≥ ,当且仅当x=
,当且仅当x= 时,等号成立.
时,等号成立.所以a<
 ,……………11分
,……………11分所求满足条件的a值为1 ……………12分

练习册系列答案
 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
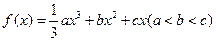 ,其图象对应的曲线设为G.(Ⅰ)设
,其图象对应的曲线设为G.(Ⅰ)设 、
、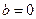 、
、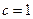 ,
,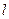 为经过点(2,2)的曲线G的切线,求
为经过点(2,2)的曲线G的切线,求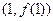 、B
、B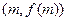 处的切线的斜率分别为0、
处的切线的斜率分别为0、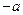 ,求证:
,求证: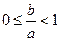 ;
;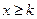 时,
时,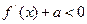 恒成立,求常数
恒成立,求常数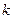 的最小值.
的最小值. ≥0)在点M(t,
≥0)在点M(t, 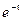 )处的切线
)处的切线 与x轴y轴所围成的三角形面积为
与x轴y轴所围成的三角形面积为 ,
, ]上取得最大值时,x的值为 ( )
]上取得最大值时,x的值为 ( )

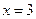 是函数
是函数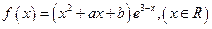 的一个极值点。
的一个极值点。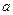 与
与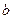 的关系式(用
的关系式(用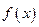 的单调区间;(2)设
的单调区间;(2)设 ,若存在
,若存在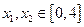 ,使得
,使得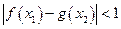 成立,求
成立,求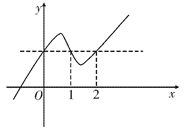 函数y=f(x)的图象如右图所示,且函数y=F(x)的图象经过(1,2)和(-1,2)两点,又过点(1,0)作斜率之积为-10的两条直线l1和l2,l1和l2与函数
函数y=f(x)的图象如右图所示,且函数y=F(x)的图象经过(1,2)和(-1,2)两点,又过点(1,0)作斜率之积为-10的两条直线l1和l2,l1和l2与函数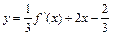 的图象分别相交于A、B两点和C、D两点,O为坐标原点。
的图象分别相交于A、B两点和C、D两点,O为坐标原点。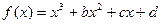 在(0,+
在(0,+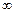 )上是增函数,在[–1,0]上是减函数,且方程
)上是增函数,在[–1,0]上是减函数,且方程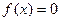 有三个根,它们分别为α,–1,β.
有三个根,它们分别为α,–1,β.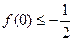 ;(3)求|α–β|的取值范围.
;(3)求|α–β|的取值范围. ,则
,则 可以是下列各式中的( )
可以是下列各式中的( )


