题目内容
(本题满分10分)
设曲线 ≥0)在点M(t,
≥0)在点M(t, 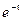 )处的切线
)处的切线 与x轴y轴所围成的三角形面积为
与x轴y轴所围成的三角形面积为 ,
,
求 的解析式.
的解析式.
设曲线
 ≥0)在点M(t,
≥0)在点M(t, 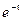 )处的切线
)处的切线 与x轴y轴所围成的三角形面积为
与x轴y轴所围成的三角形面积为 ,
,求
 的解析式.
的解析式.

 ,
, 切线
切线 的斜率为
的斜率为 ,……3分
,……3分故切线
 的方程为
的方程为 即
即 ,…… 5分
,…… 5分令y= 0得x="t+1, " x=0得
 ,… 7分
,… 7分所以S(t)=
 =
=
 .……10 分
.……10 分
练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
题目内容
 ≥0)在点M(t,
≥0)在点M(t, 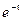 )处的切线
)处的切线 与x轴y轴所围成的三角形面积为
与x轴y轴所围成的三角形面积为 ,
, 的解析式.
的解析式.

 ,
, 切线
切线 的斜率为
的斜率为 ,……3分
,……3分 的方程为
的方程为 即
即 ,…… 5分
,…… 5分 ,… 7分
,… 7分 =
=
 .……10 分
.……10 分
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案