题目内容
11.已知二个电流瞬时值函数式分别是I1=12sin(ωt-30°),I2=10sin(ωt+30°),求合成后的电流I=I1+I2的三角函数式.分析 由题意可得I=12sin(ωt-30°)+10sin(ωt+30°),利用两角和与差的正弦函数公式,特殊角的三角函数值化简,合并同类项,利用辅助角公式即可得解.
解答 解:I=I1+I2
=12sin(ωt-30°)+10sin(ωt+30°)
=12(sinωtcos30°-cosωtsin30°)+10(sinωtcos30°+cosωtsin30°)
=6$\sqrt{3}$sinωt-6cosωt+5$\sqrt{3}$sinωt+5cosωt
=11$\sqrt{3}$sinωt-cosωt
=$\sqrt{364}$($\frac{11\sqrt{3}}{\sqrt{364}}$sinωt-$\frac{1}{\sqrt{364}}$cosωt)
=2$\sqrt{91}$sin(ωt-φ),其中cosφ=$\frac{11\sqrt{3}}{\sqrt{364}}$,sinφ=$\frac{1}{2\sqrt{91}}$.
点评 本题主要考查了两角和与差的正弦函数公式,特殊角的三角函数值,辅助角公式在三角函数化简求值中的应用,考查了转化思想,属于中档题.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
2.命题P:若x>y,则sinx>siny,在它的逆命题,否命题,逆否命三个命题中,假命题的个数为( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
12.下列函数中,既是偶函数,又是区间(0,3)内是增函数的是( )
| A. | y=log${\;}_{\frac{1}{2}}$|x| | B. | y=cosx | C. | y=ex+e-x | D. | y=x+$\frac{1}{x}$ |
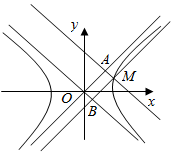 如图,设M为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)上任意一点,O为原点,过点M作双曲线两渐近线的平行线,分别与两渐近线交于A,B两点,探求平行四边形MAOB的面积,由此可以发现什么结论?
如图,设M为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)上任意一点,O为原点,过点M作双曲线两渐近线的平行线,分别与两渐近线交于A,B两点,探求平行四边形MAOB的面积,由此可以发现什么结论?