题目内容

已知函数y=x2-bx+2（x∈（-∞，1））是单调函数，则b的取值范围是______．
∵函数y=x2-bx+2的对称轴是x=
b
2
，
又∵函数y=x2-bx+2，（x∈（-∞，1））是单调函数，
又∵函数图象开口向上，
∴函数y=x2-bx+2（x∈（-∞，1））是单调减函数，
∴1≤
b
2
，
∴b≥2，
∴b的取值范围是[2，+∞）．
故答案为：[2，+∞）．
练习册系列答案
相关题目
已知二次函数f（x）是定义在R上的偶函数，且关于x的不等式f（x）＜4x的解集为{x|1＜x＜3}．
（Ⅰ）求f（x）的解析式；
（Ⅱ）设F（x）=f（x）+bx，且当x∈[-1，2]时，函数F（x）的最小值为1，求实数b的值．
函数f（x）=2x2-mx+3，当x∈[2，+∞）时是增函数，当x∈（-∞，2]时是减函数，则f（1）=______．
已知函数f（x）=2x2+（x-a）2．
（Ⅰ）若f（x+1）为偶函数，求a的值；
（Ⅱ）若f（x）在[0，1]上有最小值9，求a的值．
关于x的不等式x2-4mx+4≥0对任意x∈[1，+∞）恒成立，则实数m的取值范围为______．
定义运算：x?y=
x(xy≥0)
y(xy＜0)
，例如：3?4=3，（-2）?4=4，则函数f（x）=x2?（2x-x2）的最大值为______．
化简（1-a）[（a-1）-2（-a）
1
2
]
1
2
=______（结果写成指数幂的形式）．
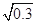已知a＝，b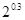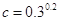＝，，则a，b，c三者的大小关系是(    )
A．b>c>aB．b>a>cC．a>b>cD．c>b>a
设a>0且a≠1，函数y＝a2x＋2ax－1在[－1,1]上的最大值是14，求a的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网