题目内容
定义运算：x?y=
，例如：3?4=3，（-2）?4=4，则函数f（x）=x2?（2x-x2）的最大值为______．
|
由x2=2x-x2，得x2=x，解得x=0或x=1，
由y=2x-x2≥0，得0≤x≤2，
由y=2x-x2＜0，得x＜0或x＞2，
∴由x2（2x-x2）≥0时，
解得0≤x≤2，
由x2（2x-x2）＜0
解得x＜0或x＞2，
即当0≤x≤2时，f（x）=x2，
当x＜0或x＞2时，f（x）=2x-x2．
作出对应的函数图象
∴图象可知当x=2时，函数f（x）取得最大值f（2）=4．
故答案为：4．
由y=2x-x2≥0，得0≤x≤2，
由y=2x-x2＜0，得x＜0或x＞2，
∴由x2（2x-x2）≥0时，
解得0≤x≤2，
由x2（2x-x2）＜0
解得x＜0或x＞2，
即当0≤x≤2时，f（x）=x2，
当x＜0或x＞2时，f（x）=2x-x2．
作出对应的函数图象
∴图象可知当x=2时，函数f（x）取得最大值f（2）=4．
故答案为：4．
练习册系列答案
相关题目
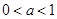时，在同一坐标系中，函数
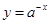与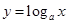
的图像是（ ）
