题目内容
(本题分12分)
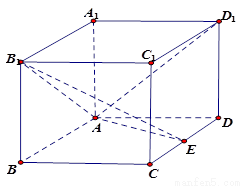
如图,在长方体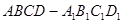 中,
中,
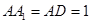 ,
, 为
为 中点.
中点.
(Ⅰ)求证: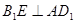 ;
;
(Ⅱ)在棱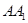 上是否存在一点
上是否存在一点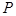 ,使得
,使得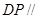 平面
平面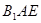 ?若存在,求
?若存在,求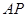 的长;若不存在,说明理由.
的长;若不存在,说明理由.
(Ⅲ)若二面角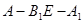 的大小为
的大小为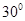 ,求
,求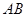 的长.
的长.
【答案】
(Ⅰ)见解析;(Ⅱ) ;
;
(Ⅲ)
【解析】本题考查利用空间向量这一工具求二面角,证明线面平行及线线垂直,解题的关键是建立恰当的坐标系及空间位置关系与向量的对应,此类解题,方法简单思维量小,但计算量大,易因为计算错误导致解题失败,解题时要严谨,认真,利用空间向量求解立体几何题是近几年高考的热点,必考内容,学习时要好好把握
(Ⅰ)由题意及所给的图形,可以A为原点,AB,AD,AA1
的方向为X轴,Y轴,Z轴的正方向建立空间直角坐标系,设AB=a,给出图形中各点的坐标,可求出向量 AD,B1E的坐标,验证其数量积为0即可证出两线段垂直
(II)由题意,可先假设在棱AA1上存在一点P(0,0,t),使得DP∥平面B1AE,求出平面B1AE法向量,可法向量与直线DP的方向向量内积为0,由此方程解出t的值,若能解出,则说明存在,若不存在符合条件的t的值,说明不存在这样的点P满足题意.
(III)由题设条件,可求面夹二面角的两个平面的法向量,利用两平面的夹角为30°建立关于a的方程,解出a的值即可得出AB的长
解:(Ⅰ)长方体 中,
中,
得:

 面
面
 面
面
 -----------4分
-----------4分
(Ⅱ)取 的中点为
的中点为 ,
, 中点为
中点为 ,连接
,连接
在 中,
中, 面
面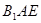
此时 -----------------------8分
-----------------------8分
(Ⅲ)设 ,连接
,连接 ,过点
,过点 作
作 于点
于点 ,连接
,连接
 面
面 ,
,

得: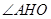 是二面角
是二面角 的平面角
的平面角
在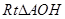 中,
中,
在矩形 中,
中,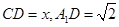


练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
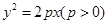 的焦点,与抛物线交于两点A、B, 将直线
的焦点,与抛物线交于两点A、B, 将直线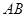 按向量
按向量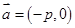 平移得到直线
平移得到直线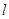 ,
,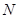 为
为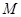 为抛物线弧
为抛物线弧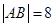 ,求抛物线方程.
,求抛物线方程.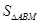 的最大值.
的最大值.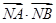 的最小值.
的最小值.
 O方程为
O方程为 ,点P在圆上,点D在x轴上,点M在DP延长线上,
,点P在圆上,点D在x轴上,点M在DP延长线上, .且
.且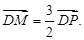
 ,若过F1的直线交(I)中曲线C于A、B两点,求
,若过F1的直线交(I)中曲线C于A、B两点,求 的取值范围.
的取值范围.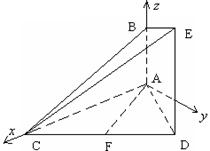
 平面
平面 ,
, ,
, ,
, ,
, .
.
 平面
平面 ;
; 的大小;
的大小; 的体
的体