题目内容
（本题满分12分）
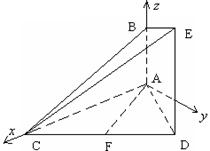
如右图，已知AB⊥平面ACD，DE⊥平面ACD，
△ACD为等边三角形，AD＝DE＝2AB，F为CD的中点．
(1)求证：AF∥平面BCE；
(2)求直线BF和平面BCE所成角的正弦值
【答案】
解：设
，建立如图所示的坐标系
，则
．
∵
为
的中点，∴
．……………2分
(1)证明： 
，
∵
，
平面BCE，∴AF∥平面BCE．
或求出平面
的法向量，再证AF与法向量垂直。……………6分
(2)解：设平面的法向量为
，由
可得：
，取
．………………………………8分
又
，设
和平面所成的角为
，
则sin
＝
＝
．
∴直线和平面所成角的正弦值为．……………………12分
【解析】略
练习册系列答案
小学学习好帮手系列答案
小学同步三练核心密卷系列答案
相关题目
是首项为
，公比
的等比数列，，
，数列
.
的通项公式；（2）求数列
的前n项和Sn.
<1，xÎR }．
，求实数a的取值范围．
（
，
为常数），且方程
有两个实根为
.
的解析式；
中，四边形
是边长为
的正方形，
，
为
上的点，且
⊥平面
⊥平面
的大小；
到平面