题目内容
(本题分12分)
如图,斜率为1的直线过抛物线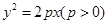 的焦点,与抛物线交于两点A、B, 将直线
的焦点,与抛物线交于两点A、B, 将直线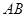 按向量
按向量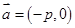 平移得到直线
平移得到直线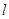 ,
,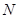 为
为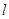 上的动点,
上的动点,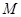 为抛物线弧
为抛物线弧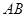 上的动点.
上的动点.
(Ⅰ)
若 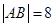 ,求抛物线方程.
,求抛物线方程.
(Ⅱ)求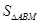 的最大值.
的最大值.
(Ⅲ)求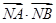 的最小值.
的最小值.

【答案】
(1) . (2)
. (2)  .
.
(3)当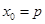 时,
时,  的最小值为
的最小值为 .
.
【解析】此题考查抛物线的定义,及向量坐标运算
(1)根据抛物线的定义得到|AB|=x1+x2+p=4p,再由已知条件,得到抛物线的方程;(2)设直线l的方程及N点坐标和A(x1,y1),B(x2,y2),利用向量坐标运算,求得

的以N点坐标表示的函数式,利用二次函数求最值的方法,可求得所求的最小值.
解:(1)由条件知 ,则
,则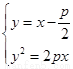 ,消去
,消去 得:
得: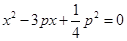 ①,则
①,则 ,由抛物线定义
,由抛物线定义 ,
,
又因为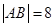 ,即
,即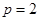 ,则抛物线方程为
,则抛物线方程为 .-------------3分
.-------------3分
(2)由(1)知 和
和 ,设
,设 ,则
,则 到
到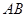 距离:
距离:
 ,因
,因 在直线
在直线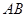 的同侧,所以
的同侧,所以 ,
,
则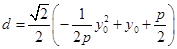 ,即
,即 ,
,
由①知
所以 ,则当
,则当 时,
时,  ,
,
则 .----------------------8分
.----------------------8分
(3) 设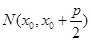 ,
,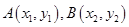 ,
,
则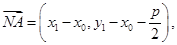
 ,
,
即
由①知 ,
, ,
, ,
, ,则
,则 ,即
,即 ,当
,当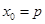 时,
时,  的最小值为
的最小值为 .
.
(其它方法酌情给分)-------- ------12分

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 中,
中,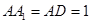 ,
,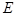 为
为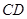 中点.
中点.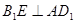 ;
;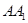 上是否存在一点
上是否存在一点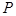 ,使得
,使得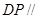 平面
平面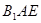 ?若存在,求
?若存在,求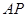 的长;若不存在,说明理由.
的长;若不存在,说明理由.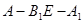 的大小为
的大小为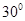 ,求
,求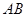 的长.
的长.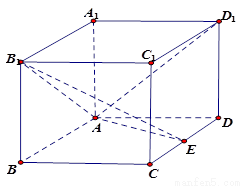
 O方程为
O方程为 ,点P在圆上,点D在x轴上,点M在DP延长线上,
,点P在圆上,点D在x轴上,点M在DP延长线上, .且
.且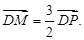
 ,若过F1的直线交(I)中曲线C于A、B两点,求
,若过F1的直线交(I)中曲线C于A、B两点,求 的取值范围.
的取值范围.
 平面
平面 ,
, ,
, ,
, ,
, .
.
 平面
平面 ;
;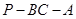 的大小;
的大小;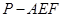 的体
的体