题目内容
设a=log3π,b=log2
,c=log3
,则a,b,c的大小关系是
| 3 |
| 2 |
a>b>c
a>b>c
.分析:由条件可得a>1,b∈(0,1),c∈(0,1),再由
=
>1,可得a,b,c的大小关系.
| b |
| c |
| lg3 |
| lg2 |
解答:解:由题意得a=log3π>log33=1,b=log2
∈(0,1),c=log3
∈(0,1),
又
=
÷
=
×
=
=
=
>1,
故有 a>b>c,
故答案为 a>b>c.
| 3 |
| 2 |
又
| b |
| c |
lg
| ||
| lg2 |
lg
| ||
| lg3 |
lg
| ||
| lg2 |
| lg3 | ||
lg
|
3lg
| ||
3lg
|
lg
| ||
lg
|
| lg3 |
| lg2 |
故有 a>b>c,
故答案为 a>b>c.
点评:本题主要考查对数函数的单调性和特殊点,比较对数值大小的方法,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设a=log3π,b=log2
,c=log3
,则( )
| 3 |
| 2 |
| A、a>b>c |
| B、a>c>b |
| C、b>a>c |
| D、b>c>a |
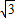 ,c=log
,c=log
 ,则( )
,则( )