题目内容

设a=log3π，b=log2
3
，c=log3
2
，则（　　）
A、a＞b＞c
B、a＞c＞b
C、b＞a＞c
D、b＞c＞a
分析：利用对数函数y=logax的单调性进行求解．当a＞1时函数为增函数当0＜a＜1时函数为减函数，
如果底a不相同时可利用1做为中介值．
解答：解：∵log3
2
＜log2
2
＜log2
3
∴b＞c
∵log2
3
＜log22=log33＜log3π∴a＞b∴a＞b＞c，故选A
点评：本题考查的是对数函数的单调性，这里需要注意的是当底不相同时可用1做为中介值．
练习册系列答案
相关题目
设a=log3π，b=log2
3
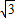，c=log
1
3
2
，则（　　）
设a=log3π，b=log2
3
，c=log3
2
，则a，b，c的大小关系是
a＞b＞c
a＞b＞c
．
设a=log3π，b=logπ3，c=log34，则a，b，c的大小顺序是
b＜a＜c
b＜a＜c
．（用“＜”连接）
设a=log3π，b=log2，c=log，则（ ）
A．a＞b＞c
B．a＞c＞b
C．b＞a＞c
D．b＞c＞a

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网