题目内容
已知平面上直线l的方向向量 =(-
=(- ,
, ),点O(0,0)和A(1,-2)在l上的射影分别是O'和A′,则
),点O(0,0)和A(1,-2)在l上的射影分别是O'和A′,则 =λe,其中λ等于
=λe,其中λ等于
- A.
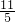
- B.-
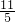
- C.2
- D.-2
D
分析:由于 在直线l上,而
在直线l上,而 为直线l的方向向量,则
为直线l的方向向量,则 ∥
∥ ,则存在实数λ,使
,则存在实数λ,使 =λ
=λ ,由
,由 与
与 的方向及模长易求出λ值.
的方向及模长易求出λ值.
解答:∵O(0,0)和A(1,-2)
∴ =(1,-2)
=(1,-2)
则 在l上的投影
在l上的投影 有:
有:
| |=|
|=| |=2
|=2
又由 与
与 的方向相反,
的方向相反,
| |=1
|=1
故由 =λ
=λ 得
得
λ=-2
故选D
点评:若向量 与非零向量
与非零向量 满足,
满足, =λ
=λ ,则:
,则:
当λ>0时,向量 与微量
与微量 同向,且λ=
同向,且λ= ,
,
当λ=0时,向量 =
= ,
,
当λ<0时,向量 与微量
与微量 反向,且λ=-
反向,且λ=- .
.
分析:由于
 在直线l上,而
在直线l上,而 为直线l的方向向量,则
为直线l的方向向量,则 ∥
∥ ,则存在实数λ,使
,则存在实数λ,使 =λ
=λ ,由
,由 与
与 的方向及模长易求出λ值.
的方向及模长易求出λ值.解答:∵O(0,0)和A(1,-2)
∴
 =(1,-2)
=(1,-2)则
 在l上的投影
在l上的投影 有:
有:|
 |=|
|=| |=2
|=2又由
 与
与 的方向相反,
的方向相反,|
 |=1
|=1故由
 =λ
=λ 得
得λ=-2
故选D
点评:若向量
 与非零向量
与非零向量 满足,
满足, =λ
=λ ,则:
,则:当λ>0时,向量
 与微量
与微量 同向,且λ=
同向,且λ= ,
,当λ=0时,向量
 =
= ,
,当λ<0时,向量
 与微量
与微量 反向,且λ=-
反向,且λ=- .
. 
练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目


 右边的程序语句运行后,输出的S为________.
右边的程序语句运行后,输出的S为________.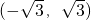

 ,则an=________.
,则an=________. ,φ∈(-π,π),则?等于
,φ∈(-π,π),则?等于

