题目内容
(本题12分)
如图1所示,在平行六面体ABCD—A1B1C1D1中,已知AB=5,AD=4,AA1=3,AB⊥AD,∠A1AB=∠A1AD= 。(1)求证:顶点A1在底面ABCD上的射影O在∠BAD的平分线上;
。(1)求证:顶点A1在底面ABCD上的射影O在∠BAD的平分线上;
(2)求这个平行六面体的体积。

图1
【答案】
(1)略
(2)平行六面体的体积为
 。
。
【解析】解(1)如图2,连结A1O,则A1O⊥底面ABCD。作OM⊥AB交AB于M,作ON⊥AD交AD于N,连结A1M,A1N。由三垂线定得得A1M⊥AB,A1N⊥AD。∵∠A1AM=∠A1AN,
∴Rt△A1NA≌Rt△A1MA,∴A1M=A1N,
从而OM=ON。
∴点O在∠BAD的平分线上。
(2)∵AM=AA1cos =3×
=3× =
=
∴AO= =
= 。
。
又在Rt△AOA1中,A1O2=AA12
– AO2=9- =
= ,
,
∴A1O= ,平行六面体的体积为
,平行六面体的体积为
 。
。













练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
 。AD=2,BC=4,AA1=2,E是DD1的中点,F是平面B1C1E
。AD=2,BC=4,AA1=2,E是DD1的中点,F是平面B1C1E
 中,
中,  ,点
,点 是棱
是棱 上一点.
上一点.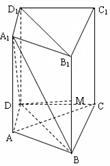
 面
面 ;
; ;
; 中,
中,  ,点
,点 是棱
是棱 上一点
上一点 面
面 ;
; ;
;
 折起,使平面ACD⊥平面ABC,得到几何体D-ABC,如图2所示.
折起,使平面ACD⊥平面ABC,得到几何体D-ABC,如图2所示.