题目内容
(本题满分15分)
已知定义在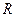 上的函数
上的函数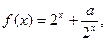
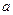 为常数,若
为常数,若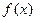 为偶函数
为偶函数
(1)求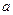 的值;
的值;
(2)判断函数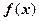 在
在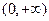 内的单调性,并用单调性定义给予证明;
内的单调性,并用单调性定义给予证明;
(3)求函数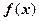 的值域.
的值域.
已知定义在
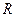 上的函数
上的函数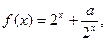
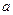 为常数,若
为常数,若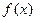 为偶函数
为偶函数(1)求
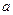 的值;
的值;(2)判断函数
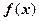 在
在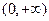 内的单调性,并用单调性定义给予证明;
内的单调性,并用单调性定义给予证明;(3)求函数
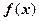 的值域.
的值域.解:(1)由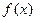 为偶函数,
为偶函数,
得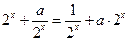 ,…………………………2分
,…………………………2分
从而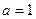 ; ……………………4分
; ……………………4分
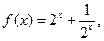 ……………………5分
……………………5分
(2)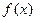 在
在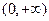 上单调增
上单调增
证明:任取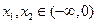 且
且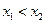 ,………………………6分
,………………………6分
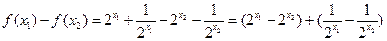
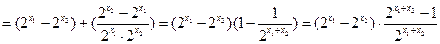 ,…………..7分
,…………..7分
当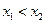 ,且
,且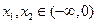 ,
,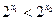 ,
,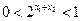 …………………………..9分
…………………………..9分
从而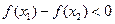 ,即
,即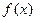 在
在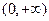 上单调增;…………………………..10分
上单调增;…………………………..10分
(3)函数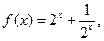
令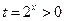 ,…………………………..11分
,…………………………..11分
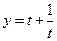
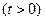 …………………………..12分
…………………………..12分
函数在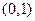 递减,在
递减,在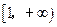 递增。(这里要简要的证明一下,假如没有证明扣1分)…..14分
递增。(这里要简要的证明一下,假如没有证明扣1分)…..14分
所以函数的值域为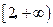 …………………………..15分
…………………………..15分
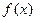 为偶函数,
为偶函数,得
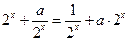 ,…………………………2分
,…………………………2分从而
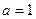 ; ……………………4分
; ……………………4分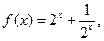 ……………………5分
……………………5分(2)
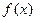 在
在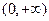 上单调增
上单调增证明:任取
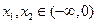 且
且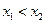 ,………………………6分
,………………………6分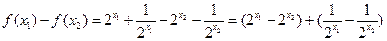
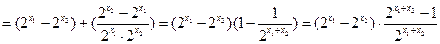 ,…………..7分
,…………..7分当
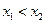 ,且
,且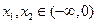 ,
,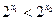 ,
,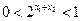 …………………………..9分
…………………………..9分从而
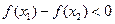 ,即
,即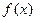 在
在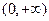 上单调增;…………………………..10分
上单调增;…………………………..10分(3)函数
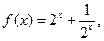
令
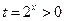 ,…………………………..11分
,…………………………..11分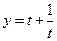
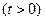 …………………………..12分
…………………………..12分函数在
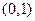 递减,在
递减,在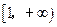 递增。(这里要简要的证明一下,假如没有证明扣1分)…..14分
递增。(这里要简要的证明一下,假如没有证明扣1分)…..14分所以函数的值域为
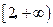 …………………………..15分
…………………………..15分略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
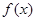 的定义域为
的定义域为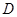 ,若存在非零实数
,若存在非零实数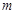 满足
满足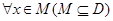 ,均有
,均有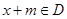 ,且
,且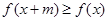 ,则称
,则称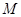 上的
上的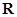 的函数
的函数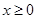 时,
时,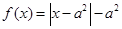 ,且
,且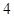 高调函数,那么实数
高调函数,那么实数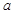 的取值范围是( )
的取值范围是( ) 



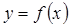 定义在
定义在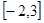 上,则函数
上,则函数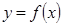 图象与直线
图象与直线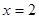 的交点个数有( )
的交点个数有( )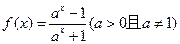
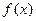 的定义域与值域;
的定义域与值域;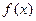 对一切实数x,y都有
对一切实数x,y都有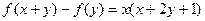 成立,且
成立,且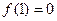 .
.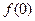 的值
的值 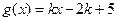 ,对任意的
,对任意的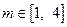 ,总存在
,总存在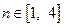 ,使得
,使得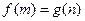 成立,求实数
成立,求实数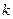 的取值范围
的取值范围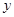 (万元)与机器运转时间
(万元)与机器运转时间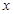 (年数,
(年数,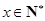 )的关系为
)的关系为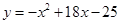 .则当每台机器运转 年时,年平均利润最大,最大值是 万元.
.则当每台机器运转 年时,年平均利润最大,最大值是 万元.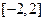 上的
上的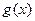 为奇函数,且在区间
为奇函数,且在区间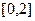 上单调递增,则满足
上单调递增,则满足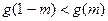 的
的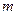 的取值范围为____ ▲ __
的取值范围为____ ▲ __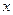 的不等式
的不等式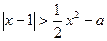 仅有负数解,则实数
仅有负数解,则实数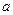 的取值范围是_________
的取值范围是_________