题目内容
(本小题满分14分)
在△ABC中,BC=2,AB+AC=3,中线AD的长为y,AB的长为x,
(1) 建立y与x的函数关系式,并指出其定义域.
(2) 求y的最小值,并指出x的值.
在△ABC中,BC=2,AB+AC=3,中线AD的长为y,AB的长为x,
(1) 建立y与x的函数关系式,并指出其定义域.
(2) 求y的最小值,并指出x的值.
解:设∠ADC=θ,则∠ADB=π-θ. 
 2分
2分
根据余弦定理得
12+y2-2ycosθ=(3-x)2,①


 4分
4分
12+y2-2ycos(π-θ)=x2. ②


 6分
6分
由①+②整理得y=



 8分
8分
其中 解得
解得 <x<
<x< .
.
∴函数的定义域为( ,
, ).
). 


 10分
10分
(2)
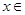 (
( ,
, )
)
 12分
12分
当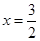 时,
时,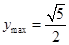



 14分
14分

 2分
2分根据余弦定理得
12+y2-2ycosθ=(3-x)2,①



 4分
4分12+y2-2ycos(π-θ)=x2. ②



 6分
6分由①+②整理得y=




 8分
8分其中
 解得
解得 <x<
<x< .
. ∴函数的定义域为(
 ,
, ).
). 


 10分
10分(2)

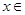 (
( ,
, )
)
 12分
12分当
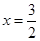 时,
时,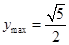



 14分
14分略

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
 ,若
,若 且
且 ,则一定有
,则一定有 



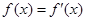 的实数根x0叫做函数
的实数根x0叫做函数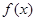 的“新驻点”,如果函数
的“新驻点”,如果函数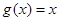 ,
,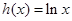 ,
,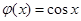 (
(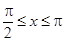 )的“新驻点”分别为
)的“新驻点”分别为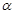 ,
,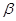 ,
,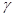 ,那么
,那么
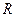 上的函数
上的函数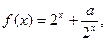
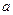 为常数,若
为常数,若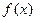 为偶函数
为偶函数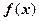 在
在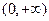 内的单调性,并用单调性定义给予证明;
内的单调性,并用单调性定义给予证明;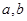 是关于
是关于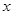 的一元二次方程
的一元二次方程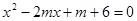 的两个实根,则
的两个实根,则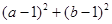 的最小值是( )
的最小值是( )


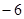
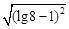 的值等于( )
的值等于( )



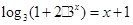 的解
的解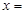 ________。
________。 ( )
( )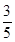
 ,
, ,
, ,则( )
,则( )


