题目内容
设函数
。
（1）若
时，函数
取得极值，求函数的图像在
处的切线方程；
（2）若函数在区间
内不单调，求实数
的取值范围。
解：①
由
得
∴
当
时，
即切点
令
得
∴切线方程为
②f(x)在区间(
,1)内不单调，即f’(x)=0在(,1)有解
∴ 3x2+2ax+1=0 2ax=-3x2-1由x∈(,1) ∴
令h(x) 
∴
知h(x)在
单调递减，在
单调递增
∴h(1)<h(x)≤
即
∴
即
而当
时，
∴舍去 综上 
练习册系列答案
相关题目
．
时函数
有三个互不相同的零点，求
的取值范围；
内没有极值点，求
的取值范围；
，不等式
在
上恒成立，求实数
．
时函数
有三个互不相同的零点，求
的取值范围；
内没有极值点，求
的取值范围；
，不等式
在
上恒成立，求实数
。
时，函数
取得极值，求函数
处的切线方程；
内不单调，求实数
的取值范围。
．
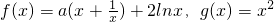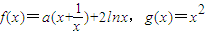时，直线l与函数f（x）和函数g（x）的图象相切于同一点，求切线l的方程；
．
时，直线l与函数f（x）和函数g（x）的图象相切于同一点，求切线l的方程；