题目内容
已知a2+4b2=2,则a+4b的最大值是______________.
![]() ∵a2+4b2=2,∴(
∵a2+4b2=2,∴(![]() )2+(
)2+(![]() b)2=1.
b)2=1.
设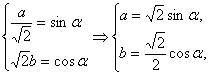 则a+4b=
则a+4b=![]() sinα+2
sinα+2![]() cosα
cosα
=![]() sin(α+φ)=
sin(α+φ)=![]() sin(α+φ)(其中tanφ=2).故a+4b的最大值为
sin(α+φ)(其中tanφ=2).故a+4b的最大值为![]() .
.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
题目内容
已知a2+4b2=2,则a+4b的最大值是______________.
![]() ∵a2+4b2=2,∴(
∵a2+4b2=2,∴(![]() )2+(
)2+(![]() b)2=1.
b)2=1.
设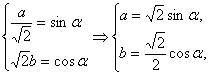 则a+4b=
则a+4b=![]() sinα+2
sinα+2![]() cosα
cosα
=![]() sin(α+φ)=
sin(α+φ)=![]() sin(α+φ)(其中tanφ=2).故a+4b的最大值为
sin(α+φ)(其中tanφ=2).故a+4b的最大值为![]() .
.

 小题狂做系列答案
小题狂做系列答案