题目内容
设集合M={x|x＜3}，N={x|x＞-2}，Q={x|x-a≥0}，令P=M∩N，若P∪Q=Q，求实数a的取值范围．
考点：交集及其运算,并集及其运算
专题：集合
分析：由已知得P={x|-2＜x＜3}，P⊆Q，由Q={x|x≥a}，能求出a≤-2．
解答：
解：∵集合M={x|x＜3}，N={x|x＞-2}，Q={x|x-a≥0}，P=M∩N，
∴P={x|-2＜x＜3}，
∵P∪Q=Q，
∴P⊆Q，
∵Q={x|x≥a}，
∴a≤-2．
∴P={x|-2＜x＜3}，
∵P∪Q=Q，
∴P⊆Q，
∵Q={x|x≥a}，
∴a≤-2．
点评：本题考查实数的取值范围的求法，解题时要认真审题，注意交集和并集的性质的合理运用．
练习册系列答案
相关题目
下列各组函数中，表示同一个函数的是（ ）
A、f（x）=
| |||
B、f（x）=logaax（a＞0，a≠1），g（x）=
| |||
C、f（x）=x，g（x）=
| |||
| D、f（x）=lnx2，g（x）=2lnx |
下列计算：①（-2014）0=1；②2m-4=
；③x4+x3=x7；④（ab2）3=a3b6；⑤
=35，正确的是（ ）
| 1 |
| 2m4 |
| (-35)2 |
| A、① | B、①②③ |
| C、①③④ | D、①④⑤ |
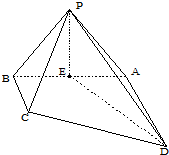如图，四棱锥P-ABCD中，底面ABCD是直角梯形，∠DAB=90°，AD∥BC，AD⊥侧面PAB，△PAB是等边三角形，DA=AB=2=0，BC=
如图，已知四棱锥P-ABCD的底面ABCD为等腰梯形，AB∥DC，AC⊥BD，AC与BD相交于点O，且顶点P在底面上的射影恰为O点，又BO=2，PO=