题目内容
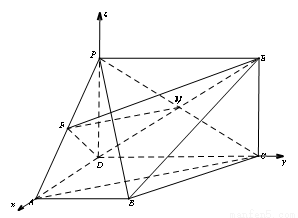
(本小题满分14分)如图,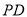 垂直于梯形
垂直于梯形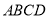 所在的平面,
所在的平面, .
. 为
为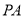 中点,
中点,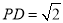 ,
,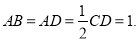 四边形
四边形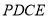 为矩形,线段
为矩形,线段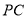 交
交 于点N .
于点N .

(1)求证: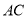 // 平面
// 平面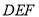 ;
;
(2)求二面角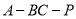 的大小;
的大小;
(3)在线段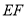 上是否存在一点
上是否存在一点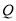 ,使得
,使得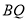 与平面
与平面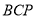 所成角的大小为
所成角的大小为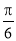 ? 若存在,请求出
? 若存在,请求出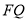 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
(1)详见解析;(2) (3)在线段
(3)在线段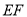 上存在一点
上存在一点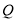 ,且
,且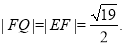
【解析】
试题分析:(1)连接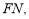 在
在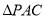 中,由题设知
中,由题设知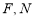 分别为
分别为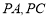 中点,所以
中点,所以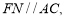 由此可证
由此可证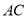 // 平面
// 平面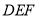 ;
;
(2)如图以 为原点,分别以
为原点,分别以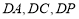 所在直线为x,y,z轴,建立空间直角坐标系
所在直线为x,y,z轴,建立空间直角坐标系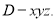 利用空间向量的数量积求出平面ABC和平面PBC的法向量的坐标,由法向量的夹角公式求出求二面角
利用空间向量的数量积求出平面ABC和平面PBC的法向量的坐标,由法向量的夹角公式求出求二面角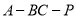 的大小;
的大小;
(3)首先假设存在点Q满足条件.由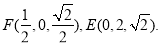 设
设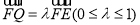 ,再利用向量的夹角公式确定
,再利用向量的夹角公式确定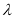 的值.
的值.
试题解析:【解析】
(Ⅰ)连接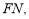 在
在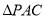 中,
中,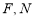 分别为
分别为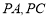 中点,所以
中点,所以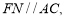
因为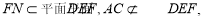
所以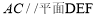 4分
4分
(2)如图以 为原点,分别以
为原点,分别以 所在直线为x,y,z轴,建立空间直角坐标系
所在直线为x,y,z轴,建立空间直角坐标系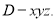 5分
5分
则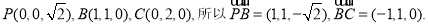
设平面 的法向量为
的法向量为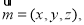 则
则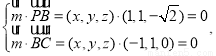
即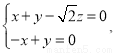 解得
解得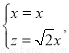
令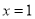 ,得
,得  所以
所以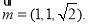 7分
7分
因为平
所以 ,
,
由图可知二面角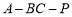 为锐二面角,
为锐二面角,
所以二面角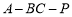 的大小为
的大小为 9分
9分
(3)设存在点Q满足条件.
由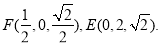 设
设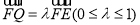 ,
,
整理得 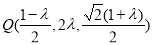 ,
, 11分
11分
因为直线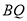 与平面
与平面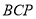 所成角的大小为
所成角的大小为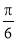 ,
,
所以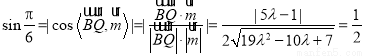 , 13分
, 13分
则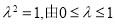 知
知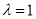 ,即
,即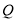 点与E点重合.
点与E点重合.
故在线段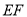 上存在一点
上存在一点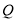 ,且
,且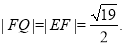 14分
14分
考点:1、空间直线与平面的位置关系;2、空间向量在解决立体几何问题中的应用.

练习册系列答案
相关题目
 ,那么
,那么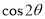 的值等于 .
的值等于 .
 表示平面,下列说法正确的是( ) .
表示平面,下列说法正确的是( ) . ,则
,则 B.若
B.若 ,则
,则
 ,则
,则 D.若
D.若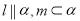 ,则
,则
 = .(
= .( 为虚数单位)
为虚数单位) )上是减函数的是
)上是减函数的是 B.
B. C.
C. D.
D.
 与
与 的夹角为
的夹角为 ,
, ,
, ,则
,则 = .
= .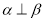 ,
, ,则
,则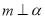
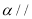
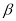 ,
,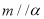 ,则
,则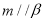
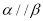 ,
,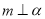 ,则
,则
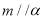 ,
,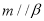 ,则
,则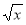 +1)=x+1,则函数f(x)的解析式为( )
+1)=x+1,则函数f(x)的解析式为( ) 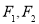 是椭圆和双曲线的公共焦点,
是椭圆和双曲线的公共焦点, 是他们的一个公共点,且
是他们的一个公共点,且 ,则椭圆和双曲线的离心率的倒数之和的最大值为
,则椭圆和双曲线的离心率的倒数之和的最大值为 B.
B.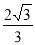 C.3 D.2
C.3 D.2