题目内容
若n-m表示[m,n](m<n)的区间长度,函数 的值域区间长度为
的值域区间长度为 ,则实数a的值为
,则实数a的值为
- A.4
- B.2
- C.

- D.1
D
分析:首先求出函数的定义域,把给出的函数式两边平方后利用配方法得到函数y2的值域,开方得到原函数的值域,利用给出的区间长度定义列式求出a的值.
解答:由 ,得0≤x≤a,所以函数f(x)的定义域为[0,a].
,得0≤x≤a,所以函数f(x)的定义域为[0,a].
令y=f(x),则y>0,且
= .
.
当x= 时,y2取最大值2a,当x=0或a时,y2取最小值a,
时,y2取最大值2a,当x=0或a时,y2取最小值a,
从而f(x)的值域为[ ,
, ],区间长度为
],区间长度为 ,
,
所以 ,解得a=1.
,解得a=1.
故选D.
点评:本题考查了函数的值域,考查了配方法,解答此题的关键是能够想到把原函数两边进行平方,是基础题.
分析:首先求出函数的定义域,把给出的函数式两边平方后利用配方法得到函数y2的值域,开方得到原函数的值域,利用给出的区间长度定义列式求出a的值.
解答:由
 ,得0≤x≤a,所以函数f(x)的定义域为[0,a].
,得0≤x≤a,所以函数f(x)的定义域为[0,a].令y=f(x),则y>0,且

=
 .
.当x=
 时,y2取最大值2a,当x=0或a时,y2取最小值a,
时,y2取最大值2a,当x=0或a时,y2取最小值a,从而f(x)的值域为[
 ,
, ],区间长度为
],区间长度为 ,
,所以
 ,解得a=1.
,解得a=1.故选D.
点评:本题考查了函数的值域,考查了配方法,解答此题的关键是能够想到把原函数两边进行平方,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
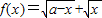 (a>0)的值域区间长度为
(a>0)的值域区间长度为 ,则实数a的值为( )
,则实数a的值为( )