题目内容

若n-m表示[m，n]（m＜n）的区间长度，函数f(x)=
a-x
+
x
(a＞0)的值域区间长度为
2
-1，则实数a的值为（　　）
A．4B．2C．
2
D．1
由
a-x≥0
x≥0
，得0≤x≤a，所以函数f（x）的定义域为[0，a]．
令y=f（x），则y＞0，且y2=(
a-x
+
x
)2=a+2
x(a-x)

=a+2
-(x-
a
2
)2+
a2
4
．
当x=
a
2
时，y2取最大值2a，当x=0或a时，y2取最小值a，
从而f（x）的值域为[
a
，
2a
]，区间长度为
2a
-
a
=
2
-1，
所以
a
(
2
-1)=
2
-1，解得a=1．
故选D．
练习册系列答案
相关题目
若 n-m表示[m，n]的区间长度，函数f(x)=
a-x
+
x
(a＞0)的值域的区间长度为2(
2
-1)，则实数a的值为
4
4
．
若n-m表示[m，n]（m＜n）的区间长度，函数f(x)=
a-x
+
x
（a＞0）的值域区间长度为2(
2
-1)，则实数a的值为（　　）
若n-m表示[m，n]（m＜n）的区间长度，函数f(x)=
a-x
+
x
(a＞0)的值域区间长度为
2
-1，则实数a的值为（　　）
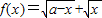若n-m表示[m，n]（m＜n）的区间长度，函数（a＞0）的值域区间长度为，则实数a的值为（ ）
A．1
B．2
C．
D．4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网