题目内容
在极坐标系中,圆C的方程为ρ=2 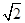 sin
sin 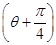 ,以极点为坐标原点,极轴为x轴的正半轴建立平面直角坐标系,直线l的参数方程为
,以极点为坐标原点,极轴为x轴的正半轴建立平面直角坐标系,直线l的参数方程为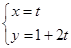 (t为参数),判断直线l和圆C的位置关系.
(t为参数),判断直线l和圆C的位置关系.
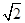 sin
sin 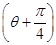 ,以极点为坐标原点,极轴为x轴的正半轴建立平面直角坐标系,直线l的参数方程为
,以极点为坐标原点,极轴为x轴的正半轴建立平面直角坐标系,直线l的参数方程为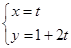 (t为参数),判断直线l和圆C的位置关系.
(t为参数),判断直线l和圆C的位置关系.相交
消去参数t,得直线l的直角坐标方程为y=2x+1;
ρ=2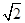
 ,即ρ=2(sin θ+cos θ),
,即ρ=2(sin θ+cos θ),
两边同乘以ρ得ρ2=2(ρsin θ+ρcos θ),
得⊙C的直角坐标方程为:(x-1)2+(x-1)2=2,
圆心C到直线l的距离d= ,所以直线l和⊙C相交.
,所以直线l和⊙C相交.
ρ=2
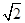
 ,即ρ=2(sin θ+cos θ),
,即ρ=2(sin θ+cos θ),两边同乘以ρ得ρ2=2(ρsin θ+ρcos θ),
得⊙C的直角坐标方程为:(x-1)2+(x-1)2=2,
圆心C到直线l的距离d=
 ,所以直线l和⊙C相交.
,所以直线l和⊙C相交.
练习册系列答案
相关题目
 的方程为
的方程为 ,以极点为坐标原点,极轴为
,以极点为坐标原点,极轴为 轴的正半轴建立平面直角坐标系,直线
轴的正半轴建立平面直角坐标系,直线 的参数方程为
的参数方程为 (
( 为参数),若直线
为参数),若直线 的值.
的值.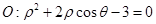 的圆心到直线
的圆心到直线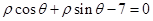 的距离是_______________.
的距离是_______________.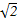 ρcos(θ-
ρcos(θ-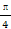 )=2.
)=2.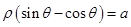 与曲线
与曲线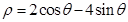 相交于
相交于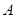 、
、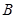 两点,若
两点,若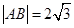 ,则实数
,则实数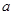 的值为 .
的值为 . 的参数方程为:
的参数方程为: (
( 为参数),圆
为参数),圆 的极坐标方程为
的极坐标方程为 ,则圆
,则圆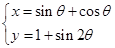 (θ为参数)有两个不同的交点,则实数a的取值范围为 .
(θ为参数)有两个不同的交点,则实数a的取值范围为 . ,那么过点P且垂直于极轴的直线的极坐标方程为
,那么过点P且垂直于极轴的直线的极坐标方程为  的圆心到直线
的圆心到直线 的距离是 .
的距离是 .