题目内容

已知椭圆的中心在原点，焦点在y轴上，若其离心率是
1
2
，焦距是8，求椭圆的方程．
考点：椭圆的标准方程
专题：圆锥曲线的定义、性质与方程
分析：由题意设椭圆的标准方程为
y2
a2
+
x2
b2
=1，a＞b＞0．且
e=
c
a
=
1
2
2c=8
a2=b2+c2
，由此能求出椭圆的方程．
解答： 解：由题意设椭圆的标准方程为
y2
a2
+
x2
b2
=1，a＞b＞0．
且
e=
c
a
=
1
2
2c=8
a2=b2+c2
，解得a2=64，b2=48，
∴椭圆的方程为
y2
64
+
x2
48
=1．
点评：本题考查椭圆方程的求法，是基础题，解题时要注意椭圆性质的合理运用．
练习册系列答案
相关题目
已知函数f（x）=ex（其中e为常用对数的底数）．
（Ⅰ）求证：f（x）≥x+1；
（Ⅱ）求证：f（x）＞ln（x+m），其中常数m≤2．
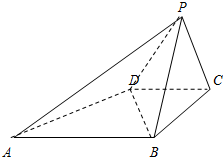如图，已知四棱锥P-ABCD的底面是直角梯形，∠ABC=∠BCD=90°，
AB=BC=PB=PC=2CD=2，侧面PBC⊥底面ABCD，
（1）求证：PA⊥BD；
（2）求二面角B-AP-D的大小．
设函数f（x）=ax2+2bx+c（a＜b＜c），函数y=f（x）的图象经过A（1，0）、B（m，-a）．
（1）若y=f（x）在x=x0处取得极值，求证：-1＜x0≤0；
（2）若f′（m）＞0，试判断f（m-2）的符号，并加以证明．
已知函数f（x）=-3x2+a（6-a）x+c．
（1）当c=19时，解关于a的不等式f（1）＞0；
（2）若关于x的不等式f（x）＞0的解集是（-1，3），求实数a，c的值．
写出双曲线和椭圆的几何定义，并标明字母符号的意义，如有必要可画图并配有文字解释．
已知奇函数f（x）的定义域为[-2，2]，且在区间[-2，0]内递减，求满足：f（1-m）+f（1-m2）＜0的实数m的取值范围．
设函数f（x）=ax3-bx2，若曲线y=f（x）在点（1，f（1））处的切线为x+y-1=0
（1）求f（x）在[-
1
2
，
3
2
]上的最大值和最小值；
（2）设g（x）=4lnx-f（x），若对任意x1，x2∈（0，+∞），当x1＜x2时，
g(x1)-g(x2)
x1-x2
≥k恒成立，求k的取值范围．
如图，圆内接三角形ABC内角平分线 CD延长后交于圆于E，若BE=2，DE=1，则CD=
 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网