题目内容
已知椭圆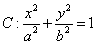
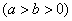 的两个焦点分别为
的两个焦点分别为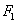 ,
,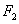 ,离心率为
,离心率为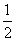 ,过
,过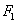 的直线
的直线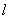 与椭圆
与椭圆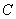 交于
交于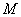 ,
,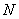 两点,且△
两点,且△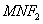 的周长为
的周长为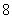 .
.
(Ⅰ)求椭圆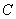 的方程;
的方程;
(Ⅱ)过原点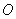 的两条互相垂直的射线与椭圆
的两条互相垂直的射线与椭圆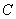 分别交于
分别交于 ,
,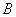 两点,证明:点
两点,证明:点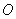 到直线
到直线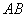 的距离为定值,并求出这个定值.
的距离为定值,并求出这个定值.
解:(I)由题意知,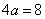 ,所以
,所以 .
.
因为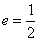
所以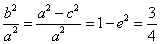 ,
,
所以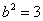 .
.
所以椭圆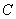 的方程为
的方程为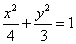 .
.
(II)由题意,当直线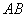 的斜率不存在,此时可设
的斜率不存在,此时可设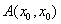 ,
,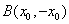 .
.
又 ,
,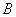 两点在椭圆
两点在椭圆 上,
上,
所以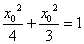 ,
,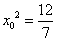 .
.
所以点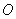 到直线
到直线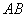 的距离
的距离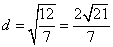 .
.
当直线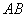 的斜率存在时,设直线
的斜率存在时,设直线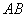 的方程为
的方程为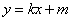 .
.
由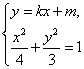 消去
消去 得
得
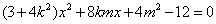 .
.
由已知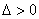 .
.
设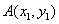 ,
,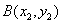 .
.
所以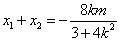 ,
,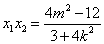 .
.
因为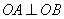 ,
,
所以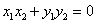 .
.
所以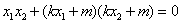 .
.
即.
所以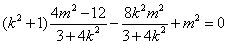 .
.
整理得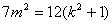 ,满足
,满足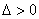 .
.
所以点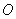 到直线
到直线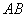 的距离
的距离
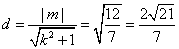 为定值.
为定值.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知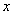 、
、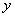 的取值如右表所示:从散点图分析,
的取值如右表所示:从散点图分析,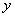 与
与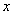 线性相关,且
线性相关,且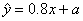 ,则
,则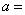 ( )
( )
A. 0.8 B. 1 C. 1.2 D. 1.5
|
| 0 | 1 | 3 | 4 |
|
| 0.9 | 1.9 | 3.2 | 4.4 |
 锥
锥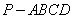 中,平面
中,平面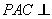 平面
平面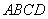 ,且
,且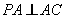 ,
, 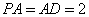 .四边形
.四边形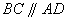 ,
,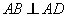 ,
,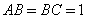 .
.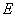 为侧棱
为侧棱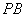 的中点,
的中点,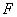 为侧棱
为侧棱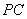 上的任意一点.
上的任意一点.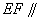 平面
平面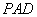 ;
;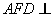 平面
平面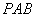 ;
;  与平面
与平面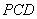 垂直?若存在,写出证明过程并求出线段
垂直?若存在,写出证明过程并求出线段 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.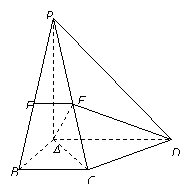
 ,直线
,直线 ,下列命题中不正确的是
,下列命题中不正确的是 ,
, ,则
,则 ∥
∥
 ∥
∥ ,
,
 ,则
,则 ,则
,则 .
. 上的函数
上的函数 的对称轴为
的对称轴为 ,且当
,且当 时,
时, .若函数
.若函数 (
( )上有零点,则
)上有零点,则 的值为
的值为 或
或 (B)
(B) (C)
(C) 或
或
 , 则位于第10行的第8列的项等于 ,
, 则位于第10行的第8列的项等于 , 在图中位于 .(填第几行的第几列)
在图中位于 .(填第几行的第几列)
 的离心率e为方程
的离心率e为方程 的根,则满足条件的圆锥曲线的个数为( )
的根,则满足条件的圆锥曲线的个数为( ) ,
,  ,
, 的零点分别是
的零点分别是 ,
, ,
, 。则( )
。则( ) <
< <
< B.
B.  为虚数单位,计算
为虚数单位,计算 =
=  .
.