题目内容
已知等差数列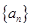 满足
满足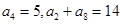 ,数列
,数列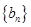 满足
满足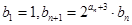 .
.
(1)求数列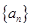 和
和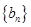 的通项公式;
的通项公式;
(2)求数列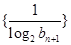 的前
的前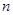 项和;
项和;
(3)若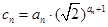 ,求数列
,求数列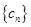 的前
的前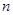 项和
项和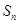 .
.
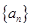 满足
满足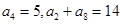 ,数列
,数列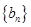 满足
满足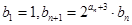 .
.(1)求数列
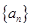 和
和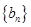 的通项公式;
的通项公式;(2)求数列
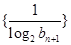 的前
的前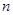 项和;
项和;(3)若
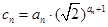 ,求数列
,求数列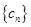 的前
的前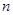 项和
项和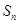 .
.(1) ,
,
(2)
(3)
 ,
,
(2)

(3)

试题分析:解:(1)
 ;
; ,
, ,以上各式相乘,得
,以上各式相乘,得 ,
, ,
, ;
;(2)
 ,
,
(3)
 ,
,




 .
.点评:主要是考查了等差数列和等比数列的求和以及通项公式的综合运用,属于中档题。

练习册系列答案
相关题目
 的前n项和为
的前n项和为 ,若
,若 ,则
,则 =( )
=( ) 的等比数列,且1-a2是a1与1+a3的等比中项,前n项和为Sn;数列{bn}是等差数列,b1=8,其前n项和Tn满足Tn=n
的等比数列,且1-a2是a1与1+a3的等比中项,前n项和为Sn;数列{bn}是等差数列,b1=8,其前n项和Tn满足Tn=n ·bn+1(
·bn+1( +
+ +
+ + +
+ + 与了
与了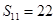 ,则
,则 ______
______ 中,
中, ,则数列
,则数列 项和
项和 取最大值时,
取最大值时, 中,
中,  则
则 ( )
( )
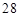

 满足:
满足: 。
。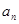 的通项公式
的通项公式 时,求证:
时,求证:
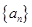 中,
中,
 的前
的前 项和为
项和为 ,常数
,常数 ,且
,且 对一切正整数
对一切正整数 ,
, ,求证:
,求证:  <4
<4