题目内容
已知点P(ρ,θ)是圆C:ρ-2sinθ=0上的动点.
(1)将曲线的极坐标方程化为直角坐标方程,并求圆心的极坐标;
(2)若P(x,y)为圆C上的一个动点,求2x+y的取值范围.
解:(1)圆 (角度不唯一
(角度不唯一 )
)
(2)设圆的参数方程为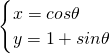 ,
,
∵
∴ ,
,
即2x+y的取值范围为 .
.
分析:(1)先在极坐标方程ρ-2sinθ=0的两边同乘以ρ,再利用直角坐标与极坐标间的关系,即利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,进行代换即得.
(2)利用圆的参数方程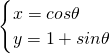 ,将求2x+y的取值范围问题转化为三角函数的最值问题加以解决.
,将求2x+y的取值范围问题转化为三角函数的最值问题加以解决.
点评:本题考查点的极坐标和直角坐标的互化,能在极坐标系中用极坐标刻画点的位置,体会在极坐标系和平面直角坐标系中刻画点的位置的区别,能进行极坐标和直角坐标的互化.
 (角度不唯一
(角度不唯一 )
) (2)设圆的参数方程为
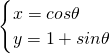 ,
,
∵

∴
 ,
,即2x+y的取值范围为
 .
.分析:(1)先在极坐标方程ρ-2sinθ=0的两边同乘以ρ,再利用直角坐标与极坐标间的关系,即利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,进行代换即得.
(2)利用圆的参数方程
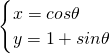 ,将求2x+y的取值范围问题转化为三角函数的最值问题加以解决.
,将求2x+y的取值范围问题转化为三角函数的最值问题加以解决.点评:本题考查点的极坐标和直角坐标的互化,能在极坐标系中用极坐标刻画点的位置,体会在极坐标系和平面直角坐标系中刻画点的位置的区别,能进行极坐标和直角坐标的互化.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知点P(m,n)是直线2x+y+5=0上的任意一点,则
的最小值为( )
| m2+n2 |
A、
| ||
B、
| ||
| C、5 | ||
| D、10 |