题目内容

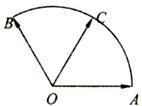已知：如图，两个长度为1的平面向量
OA
和
OB
，它们的夹角为
2π
3
，点C是以O为圆心的劣弧AB的中点．求：
（1）|
OA
+
OB
|的值；
（2）
AB
•
AC
的值．
分析：（1）根据条件先求出
OA
•
OB
的值，再求出|
OA
+
OB
|=
(
OA
+
OB
)2
的值；
（2）根据条件求出
OA
•
OC
，
OB
•
OC
的值，再由减法运算得
AB
•
AC
=（
OB
-
OA
）•（
OC
-
OA
），再展开进行求解即可．
解答：解：（1）∵
OA
和
OB
的长度为1，夹角为
2π
3
，
∴
OA
•
OB
=|
OA
||
OB
|cos
2π
3
=-
1
2
，
∴|
OA
+
OB
|=
(
OA
+
OB
)2
=
OA
2+2
OA
•
OB
+
OB
2
=1，
（2）∵点C是以O为圆心的劣弧AB的中点，
∴∠AOC=∠BOC=
π
3
，∴
OA
•
OC
=
OB
•
OC
=
1
2
，
∴
AB
•
AC
=（
OB
-
OA
）•（
OC
-
OA
）
=
OB
•
OC
-
OB
•
OA
-
OA
•
OC
+
OA
•
OA

=
1
2
-（-
1
2
）-
1
2
+1=
3
2
．
点评：本题考查了向量的数量积和减法运算，主要利用定义和性质进行求解．
练习册系列答案
相关题目
精英家教网已知等轴双曲线C的两个焦点F1、F2在直线y=x上，线段F1F2的中点是坐标原点，且双曲线经过点（3，
3
2
）．
（1）若已知下列所给的三个方程中有一个是等轴双曲线C的方程：①x2-y2=
27
4
；②xy=9；③xy=
9
2
．请确定哪个是等轴双曲线C的方程，并求出此双曲线的实轴长；
（2）现要在等轴双曲线C上选一处P建一座码头，向A（3，3）、B（9，6）两地转运货物．经测算，从P到A、从P到B修建公路的费用都是每单位长度a万元，则码头应建在何处，才能使修建两条公路的总费用最低？
（3）如图，函数y=
3
3
x+
1
x
的图象也是双曲线，请尝试研究此双曲线的性质，你能得到哪些结论？（本小题将按所得到的双曲线性质的数量和质量酌情给分）

已知：如图，两个长度为1的平面向量，它们的夹角为，点C是以O为圆心的劣弧的中点.   求：（1）的值；（2）求的值.

 

（本小题满分6分）

已知：如图，两个长度为1的平面向量，它们的夹角为，点C是以O为圆心的劣弧的中点。

 

 

求：（1）的值；（2）的值。

 
已知：如图，两个长度为1的平面向量，它们的夹角为，点C是以O为圆心的劣弧AB的中点．求：
（1）的值；
（2）的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网