题目内容
14. 如图,在底面为梯形的四棱锥S-ABCD中,已知AD∥BC,∠ASC=60°,AD=DC=$\sqrt{2}$,SA=SC=SD=2.
如图,在底面为梯形的四棱锥S-ABCD中,已知AD∥BC,∠ASC=60°,AD=DC=$\sqrt{2}$,SA=SC=SD=2.(1)求证:AC⊥SD;
(2)求点B到平面SAD的距离.
分析 (1)取AC中点O,连结OD,SO,由等腰三角形的性质可知AC⊥SO,AC⊥OD,故AC⊥平面SOD,于是AC⊥SD;
(2)由△ASC是等边三角形可求得SO,AC,利用勾股定理的逆定理可证明AD⊥CD,SO⊥OD,故而SO⊥平面ABCD,由V棱锥B-SAD=V棱锥S-ABD,计算即可.
解答 证明:(1)取AC中点O,连结OD,SO,
∵SA=SC,∴SO⊥AC,
∵AD=CD,∴OD⊥AC,
又∵OS?平面SOD,OD?平面SOD,OS∩OD=O,
∴AC⊥平面SOD,∵SD?平面SOD,
∴AC⊥SD.
解:(2)∵SA=SC=2,∠ASC=60°,∴△ASC是等边三角形,∴AC=2,OS=$\sqrt{3}$,
∵AD=CD=$\sqrt{2}$,∴AD2+CD2=AC2,∴∠ADC=90°,OD=$\frac{1}{2}AC$=1.
∵SD=2,∴SO2+OD2=SD2,∴SO⊥OD,
又∵SO⊥AC,AC?平面ABCD,OD?平面ABCD,AC∩OD=O,∴SO⊥平面ABCD,
又s△SAD=$\frac{1}{2}×AD×\sqrt{S{A}^{2}-(\frac{AD}{2})^{2}}=\frac{\sqrt{7}}{2}$
∴V棱锥B-SAD=V棱锥S-ABD,
$\frac{1}{3}×\frac{\sqrt{7}}{2}×d=\frac{1}{3}×\frac{1}{2}×AD×CD×SO$,
解得d=$\frac{2\sqrt{21}}{7}$,
∴点B到平面SAD的距离d=$\frac{2\sqrt{21}}{7}$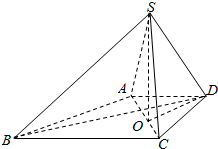
点评 题考查了线面垂直的判定与性质,棱锥的体积计算,等体积法求距离,属于中档题.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
4.设等差数列{an}的前n项和为Sn,等差数列{bn}的前n项和为Tn,若此时满足$\frac{S_n}{T_n}=\frac{n-3}{n+3}$,则$\frac{a_2}{{{b_{10}}+{b_{20}}}}+\frac{{{a_{28}}}}{{{b_{12}}+{b_{18}}}}$=( )
| A. | 1 | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{13}{16}$ |
5.曲线y=ex+1在点(0,2)处的切线与直线y=0和y=-x围成的三角形的面积为( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{3}$ |
2.函数y=2x+3在区间[1,5]上的最大值是( )
| A. | 5 | B. | 10 | C. | 13 | D. | 16 |
19.三名学生相邻坐成一排,每个学生面前的课桌上放着一枚完全相同的硬币,三人同时抛掷自己的硬币.若硬币正面朝上,则这个人站起来;若硬币正面朝下,则这个人继续坐着,那么,没有相邻的两个人站起来的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{5}{8}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{8}$ |
3.下列函数中,满足“对任意x1,x2∈(0,+∞),x1≠x2,均有$\frac{f{(x}_{1})-f{(x}_{2})}{{x}_{1}{-x}_{2}}$>0”的是( )
| A. | f(x)=2lg(x-1) | B. | f(x)=(x+1)2 | C. | f(x)=e-x | D. | f(x)=$\frac{1}{x}$ |