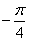题目内容
已知函数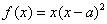 ,
,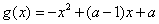 (其中
(其中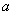 为常数);
为常数);
(Ⅰ)如果函数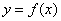 和
和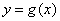 有相同的极值点,求
有相同的极值点,求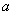 的值;
的值;
(Ⅱ)设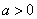 ,问是否存在
,问是否存在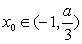 ,使得
,使得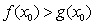 ,若存在,请求出实数
,若存在,请求出实数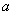 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
(Ⅲ)记函数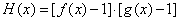 ,若函数
,若函数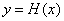 有5个不同的零点,求实数
有5个不同的零点,求实数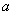 的取值范围.
的取值范围.
解:(I) ,则
,则 ,
,
令 ,得
,得 或
或 ,而
,而 在
在 处有极大值,∴
处有极大值,∴ ,或
,或 ;综上:
;综上: 或
或 .
.
(II)假设存在,即存在 ,使得
,使得

 ,
,
当 时,又
时,又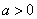 ,故
,故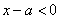 ,则存在
,则存在 ,使得
,使得 ,
,
 当
当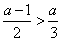 即
即 时,
时, 得
得 ,
, ;
;
 当
当 即
即 时,
时, 得
得 ,
,
 无解;综上:
无解;综上: .
.
(III)据题意有 有3个不同的实根,
有3个不同的实根, 有2个不同的实根,且这5个实根两两不相等.
有2个不同的实根,且这5个实根两两不相等.
(ⅰ) 有2个不同的实根,只需满足
有2个不同的实根,只需满足 ;
;
(ⅱ) 有3个不同的实根,
有3个不同的实根,
 当
当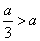 即
即 时,
时,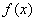 在
在 处取得极大值,而
处取得极大值,而 ,不符合题意,舍;
,不符合题意,舍;
 当
当 即
即 时,不符合题意,舍;
时,不符合题意,舍;
 当
当 即
即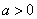 时,
时,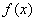 在
在 处取得极大值,
处取得极大值, ;所以
;所以 ;
;
因为(ⅰ)(ⅱ)要同时满足,故 ;(注:
;(注: 也对)
也对)
下证:这5个实根两两不相等,即证:不存在 使得
使得 和
和 同时成立;
同时成立;
若存在 使得
使得 ,
,
由 ,即
,即 ,得
,得 ,
,
当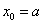 时,
时, ,不符合,舍去;
,不符合,舍去;
当 时,既有
时,既有 ①;
①;
又由 ,即
,即 ②; 联立①②式,可得
②; 联立①②式,可得 ;
;
而当 时,
时, 没有5个不同的零点,故舍去,所以这5个实根两两不相等.
没有5个不同的零点,故舍去,所以这5个实根两两不相等.
综上,当 时,函数
时,函数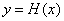 有5个不同的零点.
有5个不同的零点.

练习册系列答案
相关题目
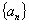 中,
中, 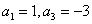
 项和
项和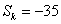 ,求
,求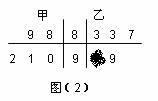
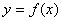
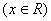 满足
满足 ,且
,且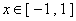 时,
时,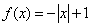 ,则当
,则当 时,
时,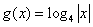 的图象的交点个数为( )
的图象的交点个数为( )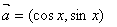 ,
,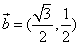 ,函数
,函数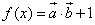 .
.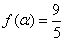 ,且
,且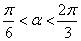 时,求
时,求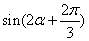 的值.
的值.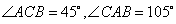 后,
后,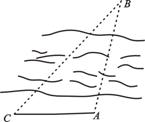 就可以计算出A、B两点的距离为( )
就可以计算出A、B两点的距离为( )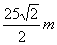 B.
B.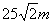
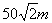 D.
D.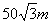
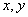 满足线性约束条件
满足线性约束条件 ,则
,则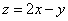 的最大值为________.
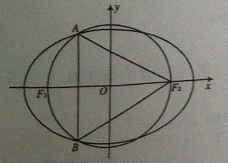
的最大值为________.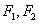 分别是椭圆
分别是椭圆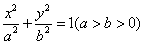 的两个焦点,
的两个焦点,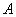 和
和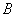 是以
是以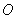 为圆心,以
为圆心,以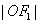 为半径的圆与该椭圆左半部分的两个交点,且△
为半径的圆与该椭圆左半部分的两个交点,且△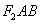 是等边三角形,则该椭圆的离心率为( )
是等边三角形,则该椭圆的离心率为( )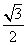 B、
B、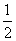 C、
C、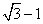 D、
D、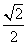
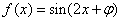 的图象沿
的图象沿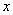 轴向左平移
轴向左平移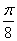 个单位后,得到一个偶函数的图象,则
个单位后,得到一个偶函数的图象,则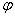 的一个可能取值为
的一个可能取值为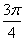 B.
B.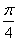 C.0 D.
C.0 D.