题目内容
边长为a的正方形ABCD沿对角线AC将△ADC折起,若∠DAB=60°,则二面角D—AC—B的大小为( )
| A.60° | B.90° | C.45° | D.30° |
B
解析试题分析:连接BD,交AC与点O,则∠DOB即为二面角D—AC—B平面角。在△DOB中,OD=OB= ,BD=
,BD= ,所以由余弦定理得:
,所以由余弦定理得: ,所以∠DOB=90°。
,所以∠DOB=90°。
考点:二面角;余弦定理。
点评:二面角求解的一般步骤: 一、“找”:找出图形中二面角,若不能直接找到可以通过作辅助线补全图形找二面角的平面角。 二、“证”:证明所找出的角就是该二面角的平面角。三、“算”:计算出该平面角。

练习册系列答案
相关题目
设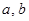 是两条直线,
是两条直线,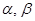 是两个不同平面,下列四个命题中,正确的命题是
是两个不同平面,下列四个命题中,正确的命题是
A.若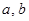 与 与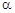 所成的角相等,则 所成的角相等,则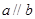 |
B.若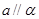 , ,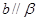 , ,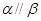 ,则 ,则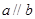 |
C.若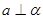 , ,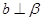 , ,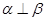 ,则 ,则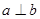 |
D.若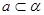 , ,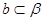 , ,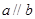 ,则 ,则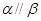 |
已知直线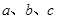 及平面
及平面 ,它们具备下列哪组条件时,有
,它们具备下列哪组条件时,有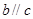 成立( )
成立( )
A.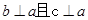 | B. |
C.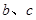 和 和 所成的角相等 所成的角相等 | D.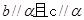 |
在正方体 中,
中, 为
为 的交点,则
的交点,则 与
与 所成角的( )
所成角的( )
A. | B.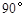 | C. | D. |
二面角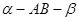 的平面角是锐角,点C
的平面角是锐角,点C 且点C不在棱AB上,D是C在平面
且点C不在棱AB上,D是C在平面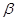 上的射影,E是棱AB上满足∠CEB为锐角的任意一点,则( )
上的射影,E是棱AB上满足∠CEB为锐角的任意一点,则( )
| A.∠CEB>∠DEB | B.∠CEB=∠DEB |
| C.∠CEB<∠DEB | D.∠CEB与∠DEB的大小关系不能确定 |
有两条不同的直线m,n与两个不同的平面α,β,下列命题正确的是( ).
| A.m∥α,n∥β,且α∥β,则m∥n |
| B.m⊥α,n⊥β,且α⊥β,则m∥n |
| C.m∥α,n⊥β,且α⊥β,则m∥n |
| D.m⊥α,n∥β,且α∥β,则m⊥n |
 的四棱锥S-ABCD的底面是边长为1的正方形,点S、A、B、C、D均在半径为1的同一球面上,则底面ABCD的中心与顶点S之间的距离为( )
的四棱锥S-ABCD的底面是边长为1的正方形,点S、A、B、C、D均在半径为1的同一球面上,则底面ABCD的中心与顶点S之间的距离为( )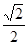 C.1 D.
C.1 D.
 中,下列几种说法正确的是 ( )
中,下列几种说法正确的是 ( )

 与
与 成
成 角
角 与
与 成
成 角
角
 、
、 为两个不同的平面,
为两个不同的平面, 、
、 、
、 为三条互不相同的直线,
为三条互不相同的直线, ,
, ,则
,则 ;
; ,
, ,
, ,
, ,则
,则 ;
; ,
, ,则
,则 ;
; ,
, ,
, ,则
,则 .
.