题目内容
过点P(1,2)的直线
(t为参数),与圆x2+y2=4相较于A、B两点,则|AB|=
|
2
| 3 |
2
.| 3 |
分析:把直线的参数方程整理为标准形式,代入圆的方程后化为直线参数的方程,利用直线参数的几何意义求解|AB|.
解答:解:由直线
,得
,
令t′=5t,则
①.
把①代入圆x2+y2=4得:(t′)2+4t′+1=0.
则t′1+t′2=-4,t′1t′2=1.
∴|AB|=|t′1-t′2|=
=
=2
.
故答案为:2
.
|
|
令t′=5t,则
|
把①代入圆x2+y2=4得:(t′)2+4t′+1=0.
则t′1+t′2=-4,t′1t′2=1.
∴|AB|=|t′1-t′2|=
| (t′1+t′2)2-4t′1t′2 |
| (-4)2-4 |
| 3 |
故答案为:2
| 3 |
点评:本题考查了直线的参数方程,考查了直线直线参数的几何意义,是基础题.

练习册系列答案
相关题目

 椭圆E:
椭圆E: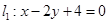 与
与 的交点为P,直
的交点为P,直 的方程为:
的方程为: .
. 过点A(a,0),B(0,b)的直
过点A(a,0),B(0,b)的直 ,原点到该直线的距离为
,原点到该直线的距离为 .
. 求直线MN的方程;
求直线MN的方程; 交椭圆于P、Q两点,以PQ为直径的圆过点D(1,0)?若存在,求出k的值;若不存在,请说明理由。
交椭圆于P、Q两点,以PQ为直径的圆过点D(1,0)?若存在,求出k的值;若不存在,请说明理由。