题目内容
12.如果α与β的正切值可能相等,我们称这两个角是“亲情角”,已知tan(β-$\frac{π}{4}$)=2,下列选项中的角与β互为“亲情角”的是( )| A. | tanα=3 | B. | sinα=$\frac{\sqrt{10}}{10}$ | C. | tan2(α+$\frac{π}{4}$)=$\frac{1}{4}$ | D. | cosα=$\frac{1}{3}$ |
分析 先求出tanβ=-3,再分别计算四个选项中的角的正切值,由此能求出与β互为“亲情角”的角.
解答 解:∵tan(β-$\frac{π}{4}$)=2,
∴$\frac{tanβ-tan\frac{π}{4}}{1+tanβtan\frac{π}{4}}=2$,解得tanβ=-3,
在A中,tanα=3≠tanβ,故A不成立;
在B中,sinα=$\frac{\sqrt{10}}{10}$,cosα=$±\sqrt{1-(\frac{\sqrt{10}}{10})^{2}}$=$±\frac{3\sqrt{10}}{10}$,tanα=$\frac{sinα}{cosα}$=$±\frac{1}{3}$,故B不成立;
在C中,tan2(α+$\frac{π}{4}$)=$\frac{1}{4}$,$tan(α+\frac{π}{4})=±\frac{1}{2}$,
当tanα=-3时,$tan(α+\frac{π}{4})$=$\frac{tanα+tan\frac{π}{4}}{1-tanαtan\frac{π}{4}}$=$\frac{-3+1}{1+3}$=-$\frac{1}{2}$,成立,故C成立;
在C中,cosα=$\frac{1}{3}$,sinα=$±\sqrt{1-(\frac{1}{3})^{2}}$=$±\sqrt{1-\frac{1}{9}}$=$±\frac{2\sqrt{2}}{3}$,
tan$α=\frac{sinα}{cosα}$=$±2\sqrt{2}$,故D不成立.
故选:C.
点评 本题考查角的求法,是基础题,解题时要认真审题,注意同角三角函数关系式和两角和与差的正弦、余弦、正切公式的合理运用.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
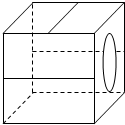
2.如图是一正方体,则其缩小的展开图是( )

| A. |  | B. | 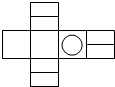 | C. | 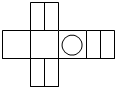 | D. |  |
3.已知点A(2,-1,5),B(t,t+1,t-1),则|AB|取得最小值时,t的值等于( )
| A. | $\sqrt{15}$ | B. | 3$\sqrt{2}$ | C. | $\sqrt{30}$ | D. | 2 |
7.在等比数列{an}中,已知a1=1,q=2,则第5项至第10项的和为( )
| A. | 63 | B. | 992 | C. | 1008 | D. | 1023 |
17.已知函数f(x)=$\sqrt{{x}^{2}-2x-3}$,则该函数的单调递增区间为( )
| A. | (-∞,1] | B. | [3,+∞) | C. | (-∞,-1] | D. | [1,+∞) |