题目内容
7.设Sn是数列{an}的前n项和,且a1=$\frac{1}{2}$,点(n,2an+1-an)(n∈N+)在直线y=x上,令bn=an+1-an-1,(1)证明:数列{an-n+2}是等比数列.
(2)求an,bn,Sn.
(3)若Sn-2bn>3n-4对n>k(k∈N+)恒成立,求k的最小值.
分析 (1)通过将点(n,2an+1-an)代入直线y=x,进而变形可知2(an+1-n-1+2)=an-n+2,从而可得结论;
(2)通过(1)可知an=n-2+$\frac{3}{{2}^{n}}$,利用分组求和法计算可知Sn=6+$\frac{1}{2}$n2-$\frac{3}{2}$n-$\frac{6}{{2}^{n}}$,代入计算可知bn=1-$\frac{3}{{2}^{n+1}}$;
(3)通过代入、化简整理可知问题转化为n2-9n+8>$\frac{6}{{2}^{n}}$对n>k(k∈N+)恒成立,通过分析不等式两端的单调性即得结论.
解答 (1)证明:∵点(n,2an+1-an)(n∈N+)在直线y=x上,
∴2an+1-an=n,2an+1=an+n,
∴2(an+1-n-1+2)=an-n+2,
又∵a1-1+2=$\frac{1}{2}$-1+2=$\frac{3}{2}$,
∴数列{an-n+2}是首项为$\frac{3}{2}$、公比为$\frac{1}{2}$的等比数列;
(2)解:由(1)可知an-n+2=$\frac{3}{{2}^{n}}$,即an=n-2+$\frac{3}{{2}^{n}}$,
∴Sn=$\frac{n(n+1)}{2}$-2n+3•$\frac{1-\frac{1}{{2}^{n}}}{1-\frac{1}{2}}$=6+$\frac{1}{2}$n2-$\frac{3}{2}$n-$\frac{6}{{2}^{n}}$,
bn=an+1-an-1=(n+1)-2+$\frac{3}{{2}^{n+1}}$-(n-2+$\frac{3}{{2}^{n}}$)=1-$\frac{3}{{2}^{n+1}}$;
(3)解:∵Sn-2bn>3n-4对n>k(k∈N+)恒成立,
∴(6+$\frac{1}{2}$n2-$\frac{3}{2}$n-$\frac{6}{{2}^{n}}$)-2(1-$\frac{3}{{2}^{n+1}}$)>3n-4对n>k(k∈N+)恒成立,
整理得:n2-9n+8>$\frac{6}{{2}^{n}}$,
∵当n取不超过8的自然数时f(n)=n2-9n+8≤0,
当n≥9时f(n)随着n的增大而增大,且f(9)=8,
而g(n)=$\frac{6}{{2}^{n}}$随着n的增大而减小,且g(8)>0、g(9)<f(9),
∴k的最小值为8.
点评 本题是一道关于数列与不等式的综合题,涉及构造等比数列、数列的单调性等基础知识,注意解题方法的积累,属于中档题.

 活力课时同步练习册系列答案
活力课时同步练习册系列答案| A. | t>5 | B. | t<5 | C. | t≥5 | D. | t≤5 |
| A. | $\frac{5π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
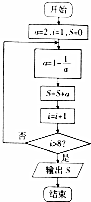
| A. | $\frac{9}{2}$ | B. | $\frac{5}{2}$ | C. | 3 | D. | $\frac{7}{2}$ |