题目内容
已知函数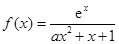 ,其中
,其中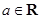 .
.
(1)若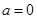 ,求函数
,求函数 的定义域和极值;
的定义域和极值;
(2)当 时,试确定函数
时,试确定函数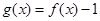 的零点个数,并证明.
的零点个数,并证明.
(1)定义域为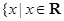 ,且
,且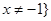 ,当
,当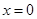 时,函数
时,函数 有极小值
有极小值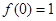 ;(2)函数
;(2)函数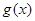 存在两个零点.
存在两个零点.
解析试题分析:若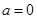 ,求函数
,求函数 的定义域和极值,把
的定义域和极值,把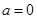 代入得函数
代入得函数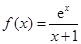 ,故可求得函数
,故可求得函数 的定义域,求它的极值,对函数求导,求出导数等于零点,及两边导数的符号,从而确定极值点;(2)当
的定义域,求它的极值,对函数求导,求出导数等于零点,及两边导数的符号,从而确定极值点;(2)当 时,试确定函数
时,试确定函数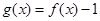 的零点个数,即求函数
的零点个数,即求函数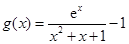 的零点个数,首先确定定义域,在定义域内,考虑函数的单调性,由单调性与根的存在性定理,来判断零点的个数.
的零点个数,首先确定定义域,在定义域内,考虑函数的单调性,由单调性与根的存在性定理,来判断零点的个数.
(1)函数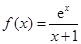 的定义域为
的定义域为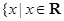 ,且
,且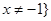 . 1分
. 1分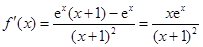 . 3分
. 3分
令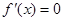 ,得
,得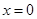 ,
,
当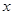 变化时,
变化时, 和
和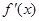 的变化情况如下:
的变化情况如下:
4分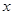
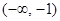
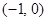

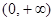
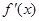
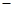


↘ ↘ ↗
故 的单调减区间为
的单调减区间为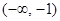 ,
,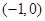

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 是
是 上的增函数,
上的增函数,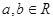 ,且
,且 ,求证
,求证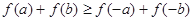
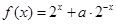
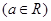 .
.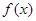 的奇偶性;
的奇偶性;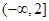 上为减函数,求
上为减函数,求 的取值范围.
的取值范围.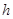 为多少时,体积V最大?最大值是多少?
为多少时,体积V最大?最大值是多少?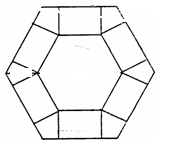
 a为常数且a>0.
a为常数且a>0. 对称;
对称; 满足条件
满足条件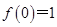 和
和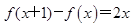 .
.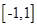 上的最大值和最小值.
上的最大值和最小值.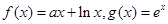 .
.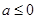 时,求
时,求 的单调区间;
的单调区间;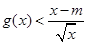 有解,求实数m的取值菹围;
有解,求实数m的取值菹围;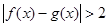 .
.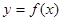 的定义域为
的定义域为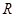 ,若存在常数
,若存在常数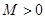 ,使得
,使得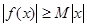 对一切实数
对一切实数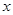 均成立,则称
均成立,则称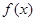 为“圆锥托底型”函数.
为“圆锥托底型”函数.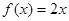 ,
,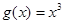 是否为“圆锥托底型”函数?并说明理由.
是否为“圆锥托底型”函数?并说明理由.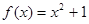 是“圆锥托底型” 函数,求出
是“圆锥托底型” 函数,求出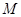 的最大值.
的最大值.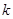 、
、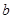 满足什么条件,
满足什么条件,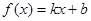 是“圆锥托底型” 函数.
是“圆锥托底型” 函数.