题目内容
17.已知数列{an}的前n项和为Sn,a1=$\frac{1}{2}$,Sn2-anSn+an=0(n≥2).(Ⅰ)求证:数列{$\frac{1}{{S}_{n}}$}是等差数列;
(Ⅱ)求S1+$\frac{1}{2}$S2+$\frac{1}{3}$S3+…+$\frac{1}{n}$Sn.
分析 (I)利用递推关系、等差数列的定义即可证明;
(II)利用等差数列的通项公式、“裂项求和”方法即可得出.
解答 证明:(Ⅰ)∵Sn2-anSn+an=0(n≥2).
∴当n≥2时,an=Sn-Sn-1,
可得:${S}_{n}^{2}$-(Sn-Sn-1)Sn+Sn-Sn-1=0,
化为:Sn-1Sn+Sn-Sn-1=0,
∴$\frac{1}{{S}_{n}}$-$\frac{1}{{S}_{n-1}}$=1,$\frac{1}{{S}_{1}}$=2.
∴数列$\{\frac{1}{{S}_{n}}\}$是以2为首项,以1为公差的等差数列.
解:(Ⅱ)由(Ⅰ)可得:$\frac{1}{{S}_{n}}$=2+(n-1)=n+1,
∴Sn=$\frac{1}{n+1}$.
∴$\frac{1}{n}{S}_{n}$=$\frac{1}{n}-\frac{1}{n+1}$.
∴S1+$\frac{1}{2}$S2+$\frac{1}{3}$S3+…+$\frac{1}{n}$Sn=$(1-\frac{1}{2})$+$(\frac{1}{2}-\frac{1}{3})$+…+$(\frac{1}{n}-\frac{1}{n+1})$
=1-$\frac{1}{n+1}$
=$\frac{n}{n+1}$.
点评 本小题主要考查an与Sn的关系、等差数列的定义与通项公式、数列求和等基础知识,考查运算求解能力,考查化归与转化思想等,属于中档题.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
8.执行如图所示的程序框图,输出k的值为( )
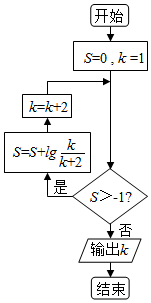

| A. | 10 | B. | 11 | C. | 12 | D. | 13 |
5.复数z满足z(1-i)=|1+i|,则复数z的共轭复数在复平面内的对应点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
2.定义A°B={x|x∈A或x∈B,但x∉A∩B}.已知M={y|y=2|x|},N={x|$\frac{3}{2-x}$≤2},则M°N=( )
| A. | [0,1)∪(2,+∞) | B. | (-∞,$\frac{1}{2}$]∪[1,2] | C. | [$\frac{1}{2}$,1)∪(2,+∞) | D. | [1,2) |
9.某程序的框图如图所示,执行该程序,若输入的N=5,则输出i=( )


| A. | 6 | B. | 7 | C. | 8 | D. | 9 |