Question

【题目】在锐角三角形中，若，则的取值范围是__________．

Answer 1

【答案】

【解析】由sinA=sin（π﹣A）=sin（B+C）=sinBcosC+cosBsinC，sinA=2sinBsinC，

可得sinBcosC+cosBsinC=2sinBsinC，①

由三角形ABC为锐角三角形，则cosB＞0，cosC＞0，

在①式两侧同时除以cosBcosC可得tanB+tanC=2tanBtanC，

又tanA=﹣tan（π﹣A）=﹣tan（B+C）=②，

则tanAtanBtanC=﹣tanBtanC，

由tanB+tanC=2tanBtanC可得tanAtanBtanC =，

令tanBtanC=t，由A，B，C为锐角可得tanA＞0，tanB＞0，tanC＞0，

由②式得1﹣tanBtanC＜0，解得t＞1，

tanAtanBtanC ，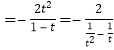

由t＞1得，﹣≤＜0，

因此tanAtanBtanC的最小值为8，