题目内容
2.在△ABC 中,角 A,B,C 的对边分别是a,b,c,若b2=a2-c2+bc,则角 A 的大小为( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
分析 利用余弦定理即可得出.
解答 解:在△ABC中,∵b2=a2-c2+bc,
∴cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=$\frac{bc}{2bc}$=$\frac{1}{2}$,
∵A∈(0,π),
∴$A=\frac{π}{3}$.
故选:B.
点评 本题考查了余弦定理的应用,考查了推理能力与技能数列,属于基础题.

练习册系列答案
相关题目
15.已知$\overrightarrow{a}$=(3,1),$\overrightarrow{b}$=(1,2),则向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
13.函数$f(x)=\sqrt{3x-{x^2}}$的定义域为( )
| A. | [-3,0] | B. | (-∞,-3]∪[0,+∞) | C. | [0,3] | D. | (-∞,0]∪[3,+∞) |
10.下列四个函数中,既是定义域上的奇函数又在区间(0,1)内单调递增的是( )
| A. | $y=\sqrt{x}$ | B. | y=-sinx | C. | $y=\frac{1}{x}$ | D. | $y=\frac{{{x^2}-1}}{x}$ |
17.若f(x)在x=x0处的导数存在,则当h→0时 $\frac{f({x}_{0}+h)-f({x}_{0}-h)}{2h}$等于( )
| A. | 2 f′(x0) | B. | $\frac{1}{2}$ f′(x0) | C. | f′(x0) | D. | 4 f′(x0) |
12.执行如图所示的程序框图,输出的S值为( )
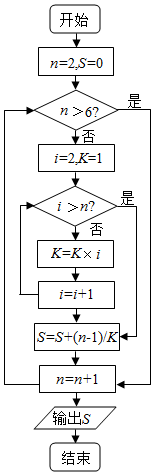

| A. | $\frac{119}{120}$ | B. | $\frac{359}{360}$ | C. | $\frac{719}{720}$ | D. | $\frac{5039}{5040}$ |