题目内容
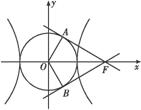
如图所示,D,E分别为△ABC的边AB,AC上的点,且不与△ABC的顶点重合.已知AE的长为m,AC的长为n,AD,AB的长是关于x的方程x2-14x+mn=0的两个根.

(1)证明:C,B, D,E四点共圆;
(2)若∠A=90°,且m=4,n=6,求C,B,D,E所在圆的半径.
(1)证明:连接DE,根据题意在△ADE和△ACB中,
AD·AB=mn=AE·AC,
即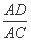 =
=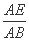 .
.
又∠DAE=∠CAB,从而△ADE∽△ACB,
因此∠ADE=∠ACB,
∴∠ACB+∠EDB=180°,
∴C、B、D、E四点共圆.
(2)解:m=4,n=6时,方程x2-14x+mn=0的两根为x1=2,x2=12,故AD=2,AB=12.
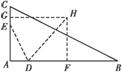
取CE的中点G,DB的中点F,分别过G、F作AC、AB的垂线,两垂线相交于H点,连接DH.
因为C、B、D、E四点共圆,
∴C、B、D、E四点所在圆的圆心为H,半径为DH.
由于∠A=90°,故GH∥AB,HF∥AC,
从而HF=AG=5,DF=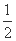 ×(12-2)=5,
×(12-2)=5,
故C、B、D、E四点所在圆的半径为5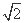 .
.

练习册系列答案
相关题目
 (B)1 (C)
(B)1 (C) 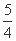 (D)
(D)
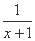 的最小值为 .
的最小值为 .  ,则线段CD的长为 .
,则线段CD的长为 . 
 ,若∠CAP=30°,则PB= .
,若∠CAP=30°,则PB= . 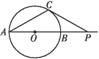
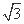 cos x(0≤x<2π)取得最大值时,x= .
cos x(0≤x<2π)取得最大值时,x= . 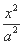 -
-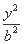 =1(a>0,b>0)的一个焦点作圆x2+y2=a2的两条切线,切点分别为A、B.若∠AOB=120°(O是坐标原点),则双曲线C的离心率为 .
=1(a>0,b>0)的一个焦点作圆x2+y2=a2的两条切线,切点分别为A、B.若∠AOB=120°(O是坐标原点),则双曲线C的离心率为 .