��Ŀ����
15����x��y����Լ������$\left\{\begin{array}{l}{x��1}\\{y��\frac{1}{2}x}\\{2x+y��10}\end{array}\right.$������$\overrightarrow{a}$=��y-2x��m����$\overrightarrow{b}$=��1��-1������$\overrightarrow{a}$��$\overrightarrow{b}$����m����СֵΪ��������| A�� | -6 | B�� | 6 | C�� | $\frac{3}{2}$ | D�� | -$\frac{3}{2}$ |
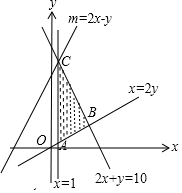
���� ���������ߵ������ʾ�õ�m=2x-y������Լ�������������������ν�����m��ֵ��
���  �⣺�������⣬����$\overrightarrow{a}$=��y-2x��m����$\overrightarrow{b}$=��1��-1����
�⣺�������⣬����$\overrightarrow{a}$=��y-2x��m����$\overrightarrow{b}$=��1��-1����
��$\overrightarrow{a}$��$\overrightarrow{b}$����-1����y-2x��-1��m=0��
��m=2x-y��
��x��y����Լ������$\left\{\begin{array}{l}{x��1}\\{y��\frac{1}{2}x}\\{2x+y��10}\end{array}\right.$�������������ͼ��
��m=2x-y����y=2x-m��
�൱ֱ��y=2x-m��y���ϵĽؾ����ʱ��m��С��
����ֱ��y=2x-m����C��1��8��ʱ��m����СֵΪ2��1-8=-6��
��ѡ��A��
���� ���⿼���˼����Թ滮���漰�������ߵ������ʾ���ؼ��Ƿ����õ�m��x��y�Ĺ�ϵ��

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ
18���躯��$f��x��=\left\{\begin{array}{l}{e^x}-��a-1��x��\;\;\;\;��x��0��\\ a-\frac{1}{x}��\;\;\;\;\;\;\;\;\;\;\;\;\;\;��x��0��\end{array}\right.$�����������x��R��f��x����x���������ʵ��a��ȡֵ��Χ�ǣ�������
| A�� | ��-2��e�� | B�� | ��-�ޣ�e�� | C�� | ��1��+�ޣ� | D�� | ��-�ޣ�1�� |
20��������z����z=��1+i������$\frac{7}{2}$$+\frac{1}{2}$i����iΪ������λ������z��ģΪ��������
| A�� | $\sqrt{5}$ | B�� | 5 | C�� | 2$\sqrt{6}$ | D�� | 25 |
7������{x��Z|��x-2����x2-3��=0}���оٷ���ʾΪ��������
| A�� | {2��$\sqrt{3}$��-$\sqrt{3}$} | B�� | {2��$\sqrt{3}$} | C�� | {2��-$\sqrt{3}$} | D�� | {2} |
4������f��x��=$\frac{{x}^{3}}{\sqrt{2-x}}$+lg��x+3���Ķ�����Ϊ��������
| A�� | ��-3��2] | B�� | [-3��2] | C�� | ��-3��2�� | D�� | ��-�ޣ�-3�� |
 ��ͼ�������ⳤ��Ϊ2��ֱ������ABCD-A��B��C��D���У�B��D���е�ΪE�䣮
��ͼ�������ⳤ��Ϊ2��ֱ������ABCD-A��B��C��D���У�B��D���е�ΪE�䣮