题目内容
3.已知当-1≤a≤1时,x2+(a-4)x+4-2a>0恒成立,则实数x的取值范围是(-∞,1)∪(3,+∞),.分析 依题意,构造函数g(a)=(x-2)a+x2-4x+4,利用一次函数的单调性质,由$\left\{\begin{array}{l}{g(-1)>0}\\{g(1)>0}\end{array}\right.$,即$\left\{\begin{array}{l}{{x}^{2}-5x+6>0}\\{{x}^{2}-3x+2>0}\end{array}\right.$,即可求出a的取值范围.
解答 解:令g(a)=(x-2)a+x2-4x+4,
∵当-1≤a≤1时,x2+(a-4)x+4-2a>0恒成立,
∴$\left\{\begin{array}{l}{g(-1)>0}\\{g(1)>0}\end{array}\right.$,即$\left\{\begin{array}{l}{{x}^{2}-5x+6>0}\\{{x}^{2}-3x+2>0}\end{array}\right.$,
解得:x>3,或x<1.
∴实数x的取值范围是:(-∞,1)∪(3,+∞),
故答案为:(-∞,1)∪(3,+∞).
点评 本题考查了函数恒成立问题,构造函数g(a)=(x-2)a+x2-4x+4是关键,突出考查等价转化思想与函数方程思想的综合运用,是易错题,难度中档.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
11.已知总体中各个体的值由小到大依次为2,3,3,7,a,b,12,15,18,20(a,b∈N*),且总体的中位数为10,若要使该总体的方差最小,则a,b的取值分别是( )
| A. | 9,11 | B. | 10,10 | C. | 8,10 | D. | 10,11 |
12.定义点P(x0,y0)到直线l:ax+by+c=0(a2+b2≠0)的有向距离为:$d=\frac{{a{x_0}+b{y_0}+c}}{{\sqrt{{a^2}+{b^2}}}}$.已知点P1、P2到直线l的有向距离分别是d1、d2.以下命题正确的是( )
| A. | 若d1=d2=1,则直线P1P2与直线l平行 | |
| B. | 若d1=1,d2=-1,则直线P1P2与直线l垂直 | |
| C. | 若d1+d2=0,则直线P1P2与直线l垂直 | |
| D. | 若d1•d2≤0,则直线P1P2与直线l相交 |
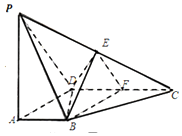 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,∠DAB为直角,AB∥CD,AD=CD=2AB=2,E,F分别为PC,CD的中点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,∠DAB为直角,AB∥CD,AD=CD=2AB=2,E,F分别为PC,CD的中点.