题目内容
如图所示,正方体ABCD—A1B1C1D1中,E是C1C的中点,则BE与平面B1BD所成角的余弦值为___________.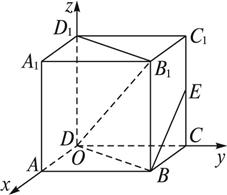
答案：
解析:如图所示建立空间直角坐标系.设正方体的棱长为2,
则B(2,2,0)、B1(2,2,2)、E(0,2,1),
=(-2,-2,0),
=(0,0,2),
=(-2,0,1).
设平面B1BD的法向量为n=(x,y,z),
因为n⊥
,n⊥
,
所以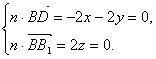
所以
令y=1,则n=(-1,1,0),cos〈n,
〉=
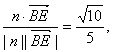
设BE与平面B1BD所成角为θ,
则cos
=sin〈n,
〉=
,
即
与平面B1BD所成角的余弦值为
.
练习册系列答案
相关题目
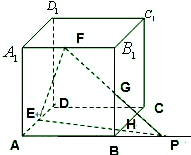如图所示，在正方体ABCD-A1B1C1D1中，其边长为2，E、F分别是AD，A1B1的中点，G、H是BB1，BC的两个动点，
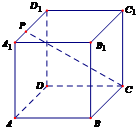如图所示，已知点P是正方体ABCD-A1B1C1D1的棱A1D1上的一个动点，设异面直线AB与CP所成的角为α，则cosα的最小值是
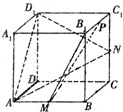如图所示，在正方体ABCD-A1B1C1D1中，AB=2，M、N分别是AB、CC1的中点，三角形MB1P的顶点P在棱C1B1上运动，给出下列结论：
