题目内容
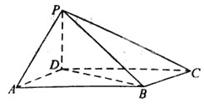
如图,在四棱锥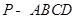 中,
中,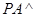 底面
底面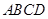 ,
,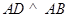 ,
,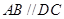 ,
,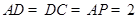 ,
,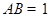 ,点
,点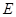 为棱
为棱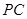 的中点.
的中点. 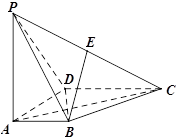
(1)证明: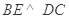 ;
;
(2)求直线 与平面
与平面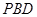 所成角的正弦值;
所成角的正弦值;
(3)若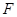 为棱
为棱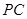 上一点,满足
上一点,满足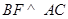 ,求二面角
,求二面角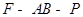 的余弦值.
的余弦值.
(1)详见试题分析;(2)直线 与平面
与平面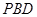 所成角的正弦值为
所成角的正弦值为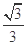 ;(3)
;(3)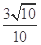 .
.
解析试题分析:(1)可以建立空间直角坐标系,利用向量数量积来证明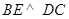 。也可以利用综合法:要证
。也可以利用综合法:要证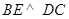 ,由于
,由于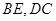 是异面直线,可将问题转化为证明线面垂直。由于点
是异面直线,可将问题转化为证明线面垂直。由于点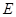 为棱
为棱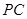 的中点,可以先取
的中点,可以先取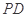 中点
中点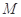 ,连结
,连结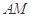 ,从而可证得
,从而可证得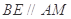 。由线面垂直的判定定理易证
。由线面垂直的判定定理易证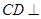 平面
平面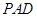 ,从而
,从而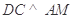 ,最后证得
,最后证得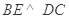 ;(2)向量法:先求平面
;(2)向量法:先求平面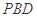 的法向量
的法向量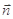 ,然后利用公式
,然后利用公式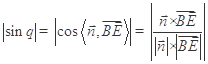 求直线
求直线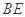 与平面
与平面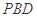 所成角的正弦值.综合法:在(I)的基础上,可先证明
所成角的正弦值.综合法:在(I)的基础上,可先证明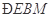 为直线
为直线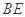 与平面
与平面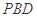 所成的角,在直角三角形
所成的角,在直角三角形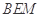 中,利用锐角三角函数即可求得直线
中,利用锐角三角函数即可求得直线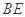 与平面
与平面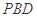 所成角的正弦值;(3)向量法:先求平面
所成角的正弦值;(3)向量法:先求平面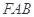 和平面
和平面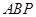 的法向量
的法向量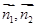 ,再利用公式
,再利用公式 来求二面角
来求二面角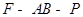 的余弦值.综合法:先利用三垂线定理或其逆定理作出二面角
的余弦值.综合法:先利用三垂线定理或其逆定理作出二面角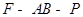 的平面角,再利用解三角形的有关知识求其余弦值.
的平面角,再利用解三角形的有关知识求其余弦值.
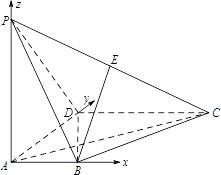
(方法一)依题意,以点 为原点建立空间直角坐标系(如图),可得
为原点建立空间直角坐标系(如图),可得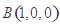 ,
,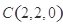 ,
,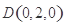 ,
,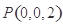 .由
.由 为棱
为棱 的中点,得
的中点,得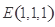 .
.
(1)向量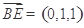 ,
,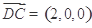 ,故
,故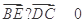 . ∴
. ∴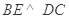 .
.
(2)向量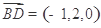 ,
,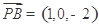 .设
.设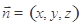 为平面
为平面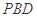 的法向量,则
的法向量,则 即
即 不妨令
不妨令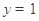 ,可得
,可得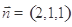 为平面
为平面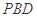 的一个法向量.于是有
的一个法向量.于是有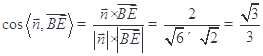 ,∴直线
,∴直线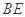 与平面
与平面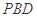 所成角的正弦值为
所成角的正弦值为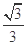 .
.
(3)向量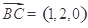 ,
,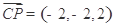 ,
,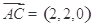 ,
,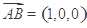 .由点
.由点 在棱
在棱 上,设
上,设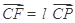 ,
,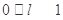 ,故
,故 ,由
,由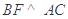 ,得
,得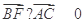 ,因此,
,因此,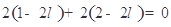 ,解得
,解得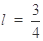 ,即
,即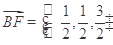 .设
.设 为平面
为平面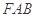 的法向量,则
的法向量,则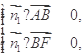 即
即

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
 ,若
,若
 ,则
,则 ______;
______;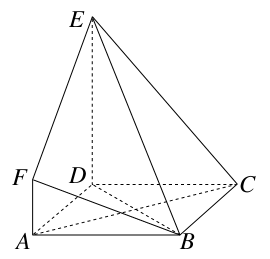
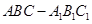 中,点
中,点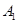 在平面ABC内的射影D在AC上,
在平面ABC内的射影D在AC上,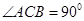 ,
,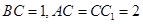 .
.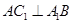 ;
;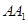 与平面
与平面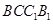 的距离为
的距离为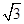 ,求二面角
,求二面角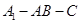 的大小.
的大小.
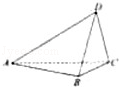
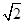 a,A1C=CA=AB=a,AB⊥AC,D为AA1中点.
a,A1C=CA=AB=a,AB⊥AC,D为AA1中点.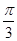 .
.
 的直径
的直径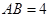 ,点
,点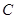 、
、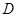 为
为 ,
,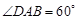 ,
,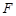 为弧
为弧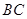 的中点.将
的中点.将 折起,使两个半圆所在平面互相垂直(如图2).
折起,使两个半圆所在平面互相垂直(如图2).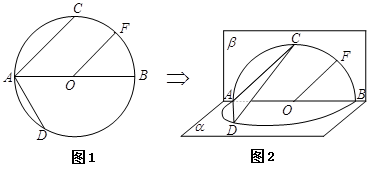
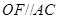 ;
;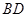 上是否存在点
上是否存在点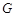 ,使得
,使得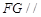 平面
平面 ?若存在,试指出点
?若存在,试指出点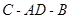 的正弦值.
的正弦值. ,
, 两点之间的距离为 .
两点之间的距离为 .