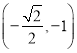题目内容
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,
,![]()
(1)求证:数列![]() 为等比数列,并求出数列
为等比数列,并求出数列![]() 的通项公式;
的通项公式;
(2)是否存在实数![]() ,对任意
,对任意![]() ,不等式
,不等式![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的取值范围,若不存在请说明理由.
的取值范围,若不存在请说明理由.
【答案】(1)证明略;![]() (2)
(2)![]()
【解析】
(1)直接利用递推关系式求出数列的通项公式,进一步证明数列为等比数列;
(2)利用(1)的结论,进一步利用分组法和恒成立问题求出实数λ的取值范围.
证明:(1)已知数列{an}的前n项和为Sn,且![]() ,①
,①
当n=1时,![]() ,
,
则:当n≥2时,![]() ,②
,②
①﹣②得:an=2an﹣2an﹣1﹣![]() +
+![]() ,
,
整理得:![]() ,
,
所以:![]() ,
,
故: (常数),
(常数),
故:数列{an}是以![]() 为首项,2为公比的等比数列.
为首项,2为公比的等比数列.
故:![]() ,
,
所以:![]() .
.
由于:![]() ,
,
所以:![]() (常数).
(常数).
故:数列{bn}为等比数列.
(2)由(1)得:![]() ,
,
所以:![]() +(
+(![]() ),
),
=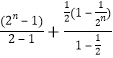 ,
,
=![]() ,
,
假设存在实数λ,对任意m,n∈N*,不等式![]() 恒成立,
恒成立,
即:![]() ,
,
由于:![]() ,
,
故当m=1时,![]() ,
,
所以:![]() ,
,
当n=1时,![]() .
.
故存在实数λ,且![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某超市为了解顾客的购物量及结算时间等信息,安排一名员工随机收集了在该超市购物的100名顾客的相关数据,如下表所示:
已知这100位顾客中一次性购物超过8件的顾客占55%.
一次性购物 | 1至4件 | 5至8件 | 9至12件 | 13至16件 | 17件及以上 |
顾客数(人) |
| 30 | 25 |
| 10 |
结算时间(分/人) | 1 | 1.5 | 2 | 2.5 | 3 |
(1)求![]() ,
,![]() 的值;
的值;
(2)求一位顾客一次购物的结算时间超过2分钟的概率(频率代替概率).