题目内容
有下面四个判断:
①命题:“设 、
、 ,若
,若 ,则
,则 ”是一个假命题
”是一个假命题
②若“p或q”为真命题,则p、q均为真命题
③命题“ 、
、 ”的否定是:
”的否定是:
“ 、
、 ”
”
④若函数 的图象关于原点对称,则
的图象关于原点对称,则
其中正确的个数共有( )
| A. 0个 | B. 1个 | C.2个 | D. 3个 |
A
解析试题分析:①的逆否命题是“若 且
且 则
则 ”,显然是一个真命题,所以原命题也是一个真命题,所以①不正确; “p或q”为真命题,可以推知p、q中至少有一个真命题,所以②不正确;“
”,显然是一个真命题,所以原命题也是一个真命题,所以①不正确; “p或q”为真命题,可以推知p、q中至少有一个真命题,所以②不正确;“ ”的否定是“
”的否定是“ ”,所以③不正确;函数
”,所以③不正确;函数 的图象关于原点对称,则该函数是奇函数,所以
的图象关于原点对称,则该函数是奇函数,所以 ,所以④不正确.
,所以④不正确.
考点:本小题主要考查命题的关系判断、命题的真值表的利用,含有一个量词的命题的否定和函数性质的应用,考查学生的推理能力.
点评:互为逆否命题的两个命题同真同假,原命题不好判断真假时,可以转为判断逆否命题的真假.

练习册系列答案
 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
已知 ,则
,则 是
是 的( )
的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
a<0是方程 至少有一个负数根的( )
至少有一个负数根的( )
| A.必要不充分条件 | B.充分不必要条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
下列有关命题的说法正确的是( )
A.命题 “若 ,则 ,则 ”的否命题为:“若 ”的否命题为:“若 ,则 ,则 ” ” |
B.“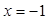 ”是“ ”是“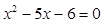 ”的必要不充分条件 ”的必要不充分条件 |
C.命题“存在 , 使得 , 使得 ”的否定是:“对任意 ”的否定是:“对任意 , 均有 , 均有 ” ” |
D.命题“若 ,则 ,则 ”的逆否命题为真命题 ”的逆否命题为真命题 |
已知P:|2x-3|<1, Q:x(x-3)<0, 则P是Q的( )
| A.充分不必要条件; | B.必要不充分条件 ; |
| C.充要条件 ; | D.既不充分也不必要条件 |
命题“若α= ,则tanα=1”的逆否命题是( )
,则tanα=1”的逆否命题是( )
A.若α≠ ,则tanα≠1 ,则tanα≠1 | B.若α= ,则tanα≠1 ,则tanα≠1 |
C.若tanα≠1,则α≠ | D.若tanα≠1,则α= |
已知命题p: ,则命题p的否定是( )
,则命题p的否定是( )
A.不存在 | B. |
C. | D. |
设甲:函数 的值域为
的值域为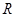 ,乙:函数
,乙:函数 有四个单调区间,那么甲是乙的
有四个单调区间,那么甲是乙的
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |


