题目内容
在直角坐标系
中，直线
的参数方程为
（
为参数）.在极坐标系（与直角坐标系取相同的长度单位，且以原点
为极点，以
轴正半轴为极轴）中，圆
的方程为
.
（1）求圆的直角坐标方程；
（2）设圆与直线交于点
，若点
的坐标为
，求
（1）
（2）
解析试题分析：（1）由得
即 (4分)
（2）将的参数方程代入圆的直角坐标方程，得
，即
(7分)
由于
，故可设
是上述方程的两实根，所以
，故由上式及的几何意义得： (10分)
考点：本题主要考查参数方程，简单曲线的极坐标方程，直线与圆的位置关系。
点评：容易题，涉及参数方程、极坐标的题目，往往难度不太大，在直线与圆锥曲线位置关系问题中，考查韦达定理应用的题目居多。
练习册系列答案
相关题目
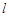的参数方程为
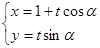(t为参数，0<a<
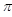)，曲线C的极坐标方程为
．
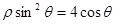为极点，以
轴的正半轴为极轴建立极坐标系，已知曲线
，过点
的直线
的参数方程为
，设直线
与曲线
分别交于
；
的普通方程；
成等比数列,求
的值．
（t为参数,O < a <
),曲线C的极坐标方程为
的最小值. 
中，把矩阵
确定的压缩变换
与矩阵
确定的旋转变换
进行复合，得到复合变换
．
在复合变换
的方程．
的参数方程为
（
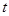为参数），
、
分别为直线
轴、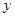
轴的交点，线段
的中点为
．
为极点，
的极坐标方程．
的解集与关于
的解集相等．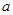
，
的值；
的最大值，以及取得最大值时
.
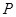是圆
上一动点，点
满足
，以极点O为原点，以极轴为x轴正半轴建立直角坐标系，求点Q的轨迹的直角坐标方程.
与直线
相切，求实数a的值。如图，在梯形
中，
，若
，
，
，则梯形
与梯形
的面积比是（ ）
A． | B． | C． | D． |