Question

8．已知函数f（x）=$\left\{\begin{array}{l}{x-{x}^{2}，-1≤x≤0}\\{x+{x}^{2}，0＜x≤1}\end{array}\right.$，若f（1-a）≤f（a），求实数a的取值范围．

Answer 1

分析 作出函数的图象，根据图象判断函数的单调性，进行求解即可．

解答 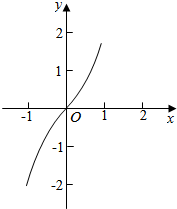解：作出函数的图象如图：则函数f（x）在[-1，1]上为增函数，
若f（1-a）≤f（a），
则$\left\{\begin{array}{l}{-1≤1-a≤1}\\{-1≤a≤1}\\{1-a≤a}\end{array}\right.$，
即$\left\{\begin{array}{l}{0≤a≤2}\\{-1≤a≤1}\\{a≥\frac{1}{2}}\end{array}\right.$，
解得$\frac{1}{2}$≤a≤1，
即实数a的取值范围是[$\frac{1}{2}$，1]．

点评 本题主要考查函数单调性的应用，根据分段函数的表达式得到函数的单调性是解决本题的关键．