题目内容
已知A={x|1＜|x-2|＜2},B={x|(x-a)(x-1)＜0,a≠1},A∩B≠
,则实数a的取值范围是_____________.
解析：A={x|0＜x＜1或3＜x＜4}.
(1)当a＞1时，B={x|(x-a)(x-1)＜0,a≠1}={x|1＜x＜a}.
又∵A∩B≠
，从下图中可知a＞3.
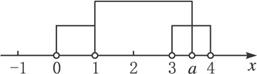
(2)当a＜1时，
B={x|(x-a)(x-1)＜0,a≠1}={x|a＜x＜1}，
又∵A∩B=
，从下图中可知a＜1.
综上所述，a的取值范围为{a|a＞3或a＜1}.
答案：{a|a＜1或a＞3}.
练习册系列答案
探究与巩固河南科学技术出版社系列答案
相关题目