题目内容

13．若函数$f（x）=\frac{4x}{x+4}{，_{\;}}且{x_1}=1，{x_{n+1}}=f（{x_n}）$，则x2017=$\frac{1}{505}$．

分析 根据数列的递推关系，构造数列{$\frac{1}{{x}_{n}}$}，得到数列{$\frac{1}{{x}_{n}}$}是等差数列，结合等差数列的通项公式进行求解即可．

解答 解：∵$f（x）=\frac{4x}{x+4}{，_{\;}}且{x_1}=1，{x_{n+1}}=f（{x_n}）$，
∴xn+1=$\frac{4{x}_{n}}{{x}_{n}+4}$，
则$\frac{1}{{x}_{n+1}}$=$\frac{{x}_{n}+4}{4{x}_{n}}$=$\frac{1}{{x}_{n}}$+$\frac{1}{4}$，
即$\frac{1}{{x}_{n+1}}$-$\frac{1}{{x}_{n}}$=$\frac{1}{4}$，
则数列{$\frac{1}{{x}_{n}}$}是公差d=$\frac{1}{4}$的等差数列，首项为1，
则$\frac{1}{{x}_{n}}$=1+$\frac{1}{4}$（n-1），
则$\frac{1}{{x}_{2017}}$=1+$\frac{1}{4}×2016$=1+504=505，
则x2017=$\frac{1}{505}$，
故答案为：$\frac{1}{505}$

点评 本题主要考查递推数列的应用，根据条件构造等差数列是解决本题的关键．综合性较强，有一定的难度．

练习册系列答案
相关题目
5．如图，在三棱锥P-ABC中，PA⊥底面ABC，∠BAC=90°．点D，E，N分别为棱PA，PC，BC的中点，M是线段AD的中点，PA=AC=4，AB=2．
（Ⅰ）求证：MN∥平面BDE；
（Ⅱ）求二面角C-EM-N的正弦值；
（Ⅲ）已知点H在棱PA上，且直线NH与直线BE所成角的余弦值为$\frac{\sqrt{7}}{21}$，求线段AH的长．
4．（1）证明：如果a＞0，b＞0，那么$\frac{a}{{\sqrt{b}}}+\frac{b}{{\sqrt{a}}}≥\sqrt{a}+\sqrt{b}$；
（2）已知2x+3y+4z=10，求x2+y2+z2的最小值．
1．已知O是三角形ABC所在平面内一定点，动点P满足$\overrightarrow{AP}=λ（\frac{{\overrightarrow{AB}}}{{|{\overrightarrow{AB}}|}}+\frac{{\overrightarrow{AC}}}{{|{\overrightarrow{AC}}|}}）λ∈{R^+}$，则P点轨迹一定通过三角形ABC的（　　）
A．内心B．外心C．垂心D．重心
8．设函数f（x）与g（x）是定义在同一区间[a，b]上的两个函数，若对任意的x∈[a，b]，都有|f（x）-g（x）|≤k（k≥0），则称f（x）与g（x）在[a，b]上是“k度和谐函数”，[a，b]称为“k度密切区间”．设函数f（x）=lnx与$g（x）=\frac{mx-1}{x}$在[$\frac{1}{e}$，e]上是“e度和谐函数”，则m的取值范围是-1≤m≤1+e．
18．设曲线f（x）=$\sqrt{{m^2}+1}cosx$（m∈R）上任一点（x，y）处切线斜率为g（x），则函数y=x2g（x）的部分图象可以为（　　）
A．B．C．D．
5．设${（{1+x+{x^2}}）^n}={a_0}+{a_1}x+{a_1}{x^2}+…+{a_{2n}}{x^{2n}}$．
（1）求a0的值；
（2）求$\frac{a_1}{2}+\frac{a_2}{2^2}+\frac{a_3}{2^3}+…+\frac{{{a_{2n}}}}{{{2^{2n}}}}$的值；
（3）求a2+a4+…+a2n的值．
2．已知函数f（x）=x2+2ax+2lnx（a∈R），g（x）=2ex+3x2（e为自然对数的底数）．
（Ⅰ）讨论函数f（x）的极值点的个数；
（Ⅱ）若函数y=f（x）的图象与函数y=g（x）的图象有两个不同的交点，求实数a的取值范围．
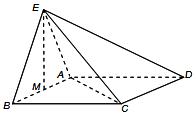3．如图，正三角形ABE与菱形ABCD所在的平面互相垂直，AB=2，∠ABC=60°，M是AB的中点．
（I）求证：EM⊥AD；
（II）求二面角A-BE-C的余弦值；
（III）在线段EC上是否存在点P，使得直线AP与平面ABE所成的角为45°，若存在，求出$\frac{EP}{EC}$的值；若不存在，说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网