题目内容
已知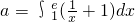 ,函数y=ax-bx(a≠b)是奇函数,则函数y=logbx是
,函数y=ax-bx(a≠b)是奇函数,则函数y=logbx是
- A.增函数
- B.减函数
- C.常数函数
- D.增函数或减函数
B
分析:利用函数的定积分求出a,利用函数的奇偶性求出b,然后通过对数函数判断函数的增减性即可.
解答:因为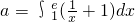 =(lnx+x)
=(lnx+x) =e,
=e,
所以函数y=ax-bx=ex-bx,
因为此函数是奇函数,所以f(-x)=-f(x),
e-x-b-x=-ex+bx, ,恒成立,所以b=
,恒成立,所以b= ,
,
所以函数y=logbx= x,函数是减函数.
x,函数是减函数.
故选B.
点评:本题考查函数的单调性与奇偶性的应用,定积分的计算,考查分析问题解决问题的能力.
分析:利用函数的定积分求出a,利用函数的奇偶性求出b,然后通过对数函数判断函数的增减性即可.
解答:因为
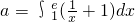 =(lnx+x)
=(lnx+x) =e,
=e,所以函数y=ax-bx=ex-bx,
因为此函数是奇函数,所以f(-x)=-f(x),
e-x-b-x=-ex+bx,
 ,恒成立,所以b=
,恒成立,所以b= ,
,所以函数y=logbx=
 x,函数是减函数.
x,函数是减函数.故选B.
点评:本题考查函数的单调性与奇偶性的应用,定积分的计算,考查分析问题解决问题的能力.

练习册系列答案
相关题目
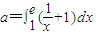 ,函数y=ax-bx(a≠b)是奇函数,则函数y=logbx是( )
,函数y=ax-bx(a≠b)是奇函数,则函数y=logbx是( )