题目内容
1.若f(x)=sinx+cosx,则f′($\frac{π}{2}$)=-1.分析 求函数的导数,利用代入法进行求解即可.
解答 解:∵f(x)=sinx+cosx,
∴f′(x)=cosx-sinx,
则f′($\frac{π}{2}$)=cos$\frac{π}{2}$-sin$\frac{π}{2}$=0-1=-1,
故答案为:-1.
点评 本题主要考查函数的导数的计算,根据函数的运算法则进行求导是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.已知i是虚数单位,复数z=$\frac{a-i}{1-i}$(a∈R),若|z|=${∫}_{0}^{π}$(sinx-$\frac{1}{π}$)dx,则a=( )
| A. | ±1 | B. | 1 | C. | -1 | D. | ±$\frac{1}{2}$ |
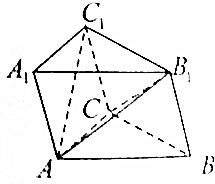 如图所示,三棱柱ABC-A1B1C1的所有棱长都相等,∠C1CB=120°.
如图所示,三棱柱ABC-A1B1C1的所有棱长都相等,∠C1CB=120°. 如图所示,秋千拉绳长3m,静止时踩板离地面高度为0.5m,某同学荡秋千时,踩板离地面最高处2m(左右对称),求该同学荡过的最大幅度AB.
如图所示,秋千拉绳长3m,静止时踩板离地面高度为0.5m,某同学荡秋千时,踩板离地面最高处2m(左右对称),求该同学荡过的最大幅度AB.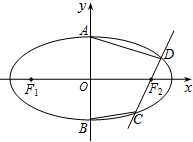 已知F1,F2分别是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左,右焦点,A,B分别为椭圆的上,下顶点.过椭圆的右焦点F2的直线在y轴右侧交椭圆于C,D两点.△F1CD的周长为8,且直线AC,BC的斜率之积为$-\frac{1}{4}$.
已知F1,F2分别是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左,右焦点,A,B分别为椭圆的上,下顶点.过椭圆的右焦点F2的直线在y轴右侧交椭圆于C,D两点.△F1CD的周长为8,且直线AC,BC的斜率之积为$-\frac{1}{4}$.